何色あれば地図が塗れる？

はじめに

世界地図では、となり合う国が別の色で塗ってあって、それぞれの形や大きさがわかりやすくなるよう工夫されています。
あらゆる地図をこのように塗るためには、何色用意すれば十分なのでしょうか？

問題の設定

問題

補足

領域が境界の点を挟んでとなり合っているとき、それらを異なる色で塗ろうとすると、地図によっては何色あっても足りない可能性があります。
そのため、境界の点でとなり合った領域は同じ色になっても構わない塗り方を考えることにします。

実際の地図では、離れた領域が同じ国や都道府県に属することがあり、それらを同じ色で塗ろうとすると、地図によっては何色あっても足りない可能性があります。
そのため、ひとかたまりの領域でなければ異なる色になっても構わない塗り方を考えることにします。
飛び地を持たない国しかない地図だけを考えるという問題として扱うこともできます。

具体例

本州の都道府県の地図を用意しました。
となり合う都道府県の色が異なるように色を塗ってみましょう。

例えば、次のように塗ることができます。
少し下にスクロールすると塗り方の例があります。

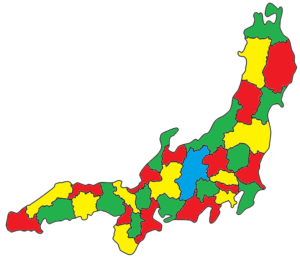
この塗り方では4色使ったので、この地図なら4色で十分だといえます。

この地図は3色以下では塗れないの？

例の塗り方では、長野県(と海)が4つ目の色である青で塗られています。
長野県が青くなってしまった原因は、となりにある群馬県，岐阜県，埼玉県，山梨県のせいなのです。
これらの県は周囲にある都道府県が奇数個になっていて、そのような領域がある地図は3色以下では塗れないことが示せます。

例えば、群馬県を見てみましょう。
群馬県を1つ目の色(赤)で塗ると、新潟県は2つ目の色(緑)で塗らなければなりません。
群馬県と新潟県にとなり合う福島県に3つ目の色(黄)を使わなければならなくなり、他もこの3色で塗らなければならないとすると、群馬県と福島県にとなり合う栃木県は緑，群馬県と栃木県にとなり合う埼玉県は黄になります。
すると、群馬県と埼玉県と新潟県にとなり合う長野県には赤も緑も黄も塗れなくなってしまいました。

つまり、本州の都道府県は3色以下では塗ることができません。
例の塗り方では、周囲の都道府県が奇数個である都道府県が必要とする4色目をすべて長野県に背負ってもらうことで完成させました。

他の地図でも4色あれば十分なの？

私たちが考えているのは、どんな地図でも塗りきれる色の数です。
周囲の領域が奇数個ある領域を持つ地図なら3色では足りませんでした。
4色では足りなくなってしまう状況も、本州の地図には偶然なかっただけで、地図によってはあるのでしょうか？

実は、4色あればどんな地図でも塗りきれるという「4色定理」が知られています。
4色定理は色々な意味で難しいのですが、もう1色増やせば塗りきれるという「5色定理」の証明は4色定理に比べればとても簡単にできます。

この記事では、5色定理の証明を解説していきます。

5色定理の証明

地図をグラフに対応させる

この記事でいうグラフとは、頂点と辺でできた図のことです。

地図の領域をグラフの頂点に対応させて、領域がとなり合っているときに対応する頂点を辺で結びます。
地図が5色以下で塗りきれることは、グラフの頂点が5色以下で塗りきれることと同じです。

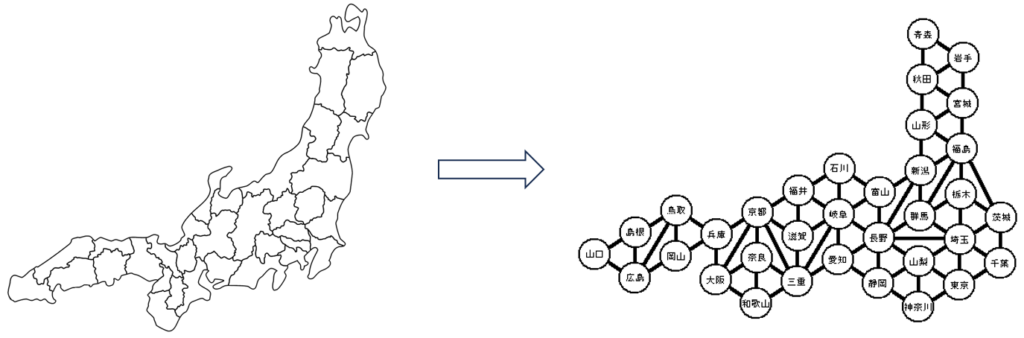
地図と対応させたグラフは次の3つの性質を持っています。

1. 連結
   グラフ全体がひとかたまりになっている。
2. 平面
   辺どうしが途中で交差しないように平面に描けている。
3. 単純
   2頂点を2つ以上の辺が結んでいたり，辺の両端が同じ頂点を結んでいたりしていない。

オイラーの多面体定理

凸多面体で成り立つオイラーの多面体定理は、連結で平面な(単純である必要はない)グラフのことばに置き換えることができます。
凸多面体の1つの面の1つの穴をあけて、拡げて伸ばしてしまえば、連結で平面なグラフにすることができるからです。
むしろ、オイラーの多面体定理はこのように置き換えて、グラフで証明されることが多いです。

価数5以下の頂点がある

頂点の価数とは、その頂点を端点にしている辺の数のことです。

地図と対応させたグラフは連結で平面なので、価数5以下の頂点を持つことが背理法によって示せます。

連結で平面なグラフに価数5以下の頂点がなかったと仮定する。
辺は頂点ごとに6つ以上あり、2回ずつ重複して数えているので、
$$2E\geq 6V$$
単純なグラフなので、辺は領域ごとに3つ以上あり、2回ずつ重複して数えているので、
$$2E\geq 3F$$
$$V−E+F\leq \frac{1}{3}E−E+\frac{2}{3}E=0$$
となり、オイラーの多面体定理に反してしまう。
よって、連結で平面なグラフには価数5以下の頂点がある。

価数5以下の頂点に色を与える

地図と対応させたグラフは価数5以下の頂点を持つ平面で単純なグラフなので、5色あれば塗れることを頂点の数に関する数学的帰納法によって示せます。

頂点が1個のとき、1色で塗れる。

頂点が\(k\)個のグラフなら5色で塗りきれると仮定する。
頂点が\(k+1\)個のグラフを考え、価数5以下の頂点があるので\(v\)とする。
\(v\)と\(v\)を端点にもつ辺を取り除いたグラフは(連結とは限らないが)頂点が\(k\)個なので帰納法の仮定から5色で塗れる。

(１)\(v\)にとなり合う頂点が4色以下で塗られているとき、\(v\)を使われていない色で塗れる。

(２)\(v\)にとなり合う頂点が異なる5色で塗られているとき、\(v\)の価数が5であり、5頂点を左回りに\(v_1, \cdots, v_5\)として、それらの色を\(c_1, \cdots, c_5\)とする。
(２-ⅰ)\(c_1\)と\(c_3\)で塗られた頂点とそれらを結ぶ辺だけを見たとき、 \(v_1\)と\(v_3\)がひとかたまりになっていないなら、\(v_3\)が含まれているかたまりの\(c_1\)と\(c_3\)を逆転させた塗り方を考えると、 \(v\)を\(c_3\)で塗ることができるようになる。
(２-ⅱ)\(v_1\)と\(v_3\)がひとかたまりになっているなら、 \(c_2\)と\(c_4\)で塗られた頂点とそれらを結ぶ辺だけを見ると、\(v_1\)と\(v_3\)のかたまりを越えることができず、 \(v_2\)と\(v_4\)はひとかたまりにならないので、\(v_4\)が含まれているかたまりの\(c_2\)と\(c_4\)を逆転させた塗り方を考えると、\(v\)を\(c_4\)で塗ることができるようになる。

よって、頂点が\(k+1\)個のグラフも5色で塗れる。

ゆえに、グラフは価数5以下の頂点を持つ平面で単純なグラフは5色で塗れる。

最後に

いかがでしたか？
色々な手順を必要とする5色定理の証明は、ちょうどいい難しさだったのではないかと思います。

興味を持ったら、強い主張である4色定理についても調べてみてください。
もしかしたら、エレガントな証明をひらめくことができるかもしれませんよ。

では、また！