目次
はじめに
てくますプロジェクトのChihiroです!
この記事では、オリジナルの論理パズルを紹介します。
本記事は、数学・情報・論理パズルを楽しむ Techmath Project Advent Calendar 2024 の10日目の記事でもあります。
アドベントカレンダーの応援や購読をしていただけると嬉しいです。
前回のパズル「アドベントカレンダーパズル(前編)」の解答を公開しました!
まだ解いていない人は前編を解いてワクワクするアドベントカレンダーに慣れておきましょう。
今回のパズルはアドベントカレンダーパズルの後編になります。
ワクワクドキドキするアドベントカレンダーの謎に挑戦してみましょう!
考えてみよう
問題

前編で13日目までが「チョコレート→キャンディー→チョコレート→クッキー→キャンディー→チョコレート→キャンディー→クッキー→キャンディー→チョコレート→クッキー→キャンディー→クッキー」だと調べたアドベントカレンダーは、全体ではこのようなルールのあるアドベントカレンダーだったのです!
入っていると書かれていなくて,前半に出てこなかっただけで、ドーナツも入っていたんですね。
「予測できない」について、例で確認してみましょう。
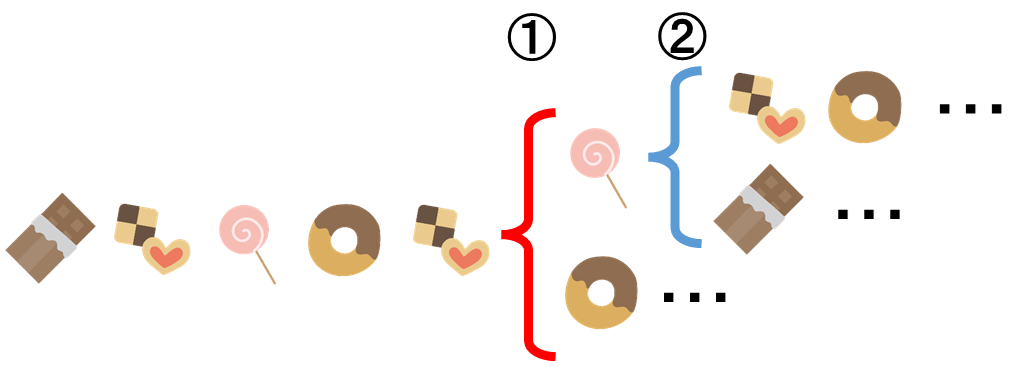
例えば、5日目までが下のような並びだとすると、クッキーの次にチョコレートが来ないように,同じパターンを繰り返さないようにするため、①のように6日目はキャンディーかドーナツになります。
6日目がキャンディーだとすると、同じパターンを繰り返さないようにするため、②のように7日目はクッキーかチョコレートになります。
7日目がクッキーだとすると、クッキーの次にチョコレートが来ないように,同じパターンを繰り返さないようにするため、8日目がドーナツで確定するので予測できてしまいます。
ということは、7日目はクッキーでないとわかり、②で7日目がチョコレートで確定するので予測できてしまいます。
ということは、6日目はキャンディーでないとわかり、①で6日目がドーナツで確定するので予測できてしまいます。
つまり、5日目までが下のような並びではないことが、「予測できない」からわかるのです。
ちなみに、この並びには13日目までにドーナツがあるので、その条件も満たしていません。
では、解いてみましょう!
アドベントカレンダーを開けている途中の人(ちひろさん)が持っている情報と、このパズルを解く人(私たち)の持っている情報の違いに注意する必要があります。
なぜなら、アドベントカレンダーのルールの「予測できない」は前者について言っているからです。
解答
ドーナツ→チョコレート→ドーナツ→キャンディー→ドーナツ→クッキー→ドーナツ→チョコレート→ドーナツ→クッキー→ドーナツ

解説
前編のように、次に来る可能性のあるお菓子を書き並べて樹形図を描きます。
しかし、後編には注意しなければならないことがあります。
それは、新しく判明したルールである「予測できない」ことです。
本来なら、実際に解答として可能性のあるお菓子の並びだけを樹形図に描いていけばいいのですが、後で「予測できない」ことを調べるために、ちひろさん目線の可能性をすべて樹形図に残す必要があります。
「4種類のお菓子が同じ数ずつ入っている」という情報はちひろさんにはありませんので、ちひろさん目線の樹形図には4種類のお菓子が同じ数ずつ入っていない並びも描かなければならないのです。
そうしなければ、次に来るお菓子がちひろさん目線では1通りではないのに1通り以外消してしまっていて、予測できてしまうように見えてその可能性も消してしまいかねないからです。
そのことに注意して、ちひろさん目線の可能性を並べた樹形図が下のようになります。
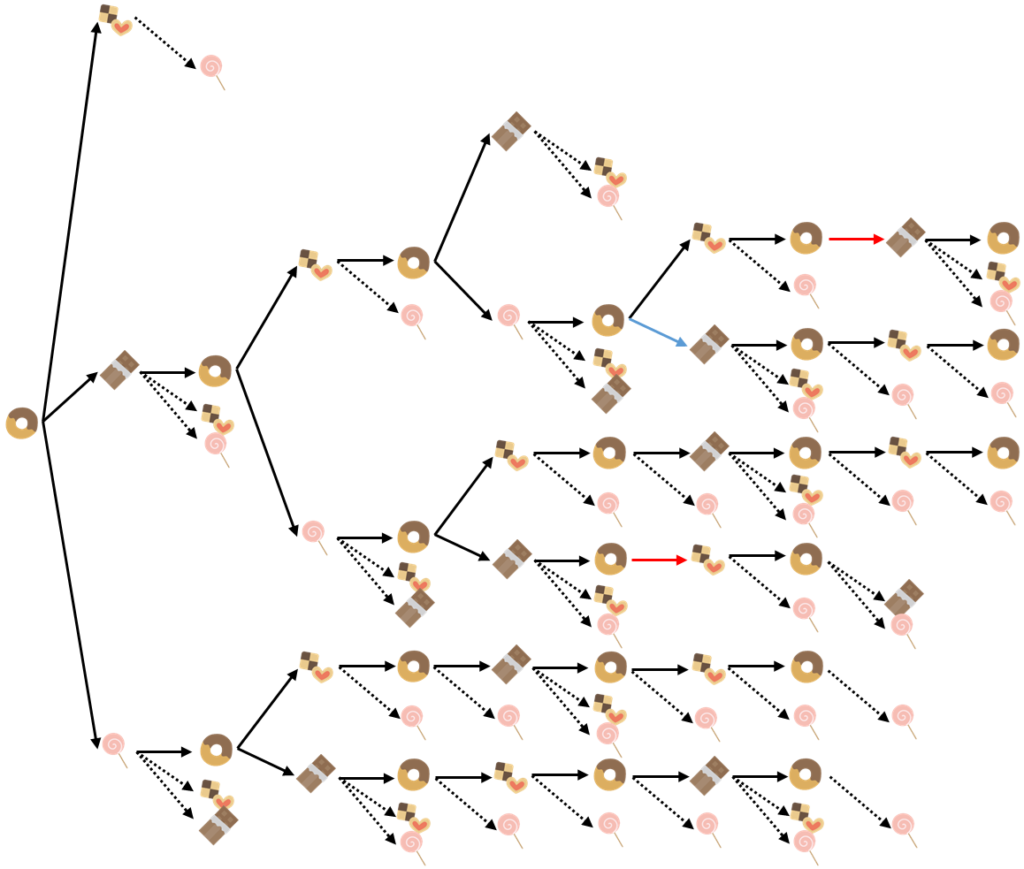
点線で描かれた矢印は、「4種類のお菓子が同じ数ずつ入っている」に反してしまうので解答にはならないがちひろさん目線ではその可能性があって、「予測できない」を正しく調べるために描いている可能性たちです。
ちひろさん目線で可能性があるからといってそのまま先まで描いていくと、どうせ解答にならないのに幅をとってしまうので、続きは省略しています。
「4種類のお菓子が同じ数ずつ入っている」を満たすためには、ドーナツを6個入れる必要があるので、「同じパターンを繰り返さない」ようにするために、ドーナツは1日置きで入れる必要がありますから、実線の矢印だけ見るとかなり可能性が絞られています。
完成した樹形図を見ると、解答の条件を満たしながら24日目まで伸ばすことのできる可能性は3通りあるように見えますが、ここから「予想できない」ことを調べていきます。
赤色で描いた矢印を見ると、ちひろさん目線でも次に来るお菓子が1通りになっていることがわかります。
なので、その並びは「予測できない」に反することとなり消すことができます。
また、これはちひろさんにも伝えられているルールなので、ちひろさん目線もその並びを可能性から消すことができます。
すると今度は、青色で描いた矢印を見ると、ちひろさん目線でも次に来るお菓子が1通りになっていることがわかります。
ドーナツ→チョコレート→ドーナツ→クッキー→ドーナツ→キャンディー→ドーナツの順で入っていたとすると、21日目がクッキーだと22日目がキャンディーだと予測できてしまうので、21日目の可能性がチョコレートだけになり予測できてしまうことになるからです。
よって、「予測できない」ことも満たすためには、「ドーナツ→チョコレート→ドーナツ→キャンディー→ドーナツ→クッキー→ドーナツ→チョコレート→ドーナツ→クッキー→ドーナツ」でなければならないことがわかります。
最後に
3種のお菓子でワクワクをギリギリまで伸ばす前編と、ドーナツとドキドキを追加してお菓子のバランスをとる後編。
一問でパズルが二度おいしいアドベントカレンダーでした!










ちひろさんが持っているワクワクドキドキなアドベントカレンダーの全貌を紹介します。
このアドベントカレンダーには次のような説明文がついていました。
・どの窓にも4種類のお菓子のうちのどれかが1つずつ入っています。
・クッキーの次の日の窓にはチョコレートは入っていません。
・ワクワクするカレンダーなので、同じパターンの繰り返しはありません。
・ドキドキするカレンダーなので、窓に何が入っているかは開けるまで予測できません。
ちひろさんが窓を開けていくと、次のことがわかりました。
・はじめの13個の窓にはドーナツは入っていませんでした。
・全体でクッキー,チョコレート,キャンディー,ドーナツが同じ数ずつ入っていました。
14~24日目の窓にはそれぞれどのお菓子が入っているでしょうか?