目次
はじめに
てくますプロジェクトのChihiroです!
前回の記事「2つの封筒問題の紹介」のパラドックス解決編を更新しました!
まずはそちらを読んでみてください。
しかし、このパラドックスの面白さはこれだけは終わりません。
この記事では、2つの封筒問題というパラドックスをさらに深く見ていきます。
本記事は、数学・情報・論理パズルを楽しむ Techmath Project Advent Calendar 2024 の13日目の記事でもあります。
アドベントカレンダーの応援や購読をしていただけると嬉しいです。
2024年3月30日の「第5回すうがく徒のつどい」にて「2つの封筒問題の整備と発展」というタイトルでさせていただいた講演の内容で、Speaker Deckに講演スライド資料を置いています。
2つの封筒問題のおさらい
2つの封筒問題というのは、次のような設定の問題です。
この問題では、「もう片方の封筒の金額の期待値を計算すると10000円より大きくなり、交換すると得である」という意見と、「10000円以外のどんな金額を確認してももう片方の封筒の金額の期待値が高いというのはおかしいので、交換しても損得はない」という意見が対立していました。
しかし、この問題には封筒に入れる金額を決める確率分布が設定されておらず、状況設定に不備があるという解決で終わったのでした。
整備された2つの封筒問題
封筒に入れる金額を設定すれば、状況設定はしっかりします。
入れる金額をコインで決めて、確率分布や事後確率が計算できるようにした問題を考えてみましょう。
コインを裏が出るまで投げ続けて、それまでに表が出た回数を\(n\)とする。
2つの封筒にそれぞれ\(3^n\)円と\(3^{n+1}\)円が入れられるが、\(n\)の値やどちらにいくら入っているかはわからない。
無作為に封筒を1つ選んで中を確認したとき、どちらの封筒を受け取ることが得であるか?
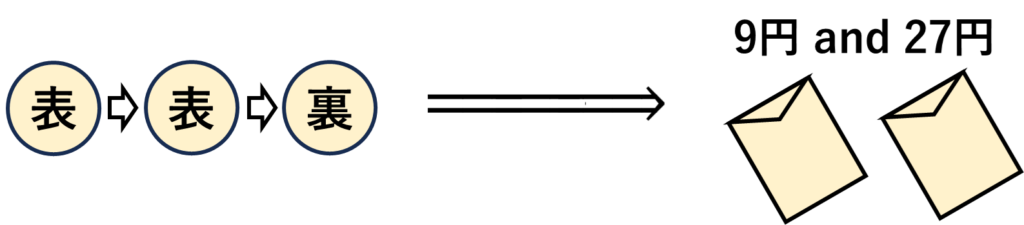
例えば、コインが表→表→裏と出た場合は、\(n=2\)となるので\(3^2=9\)円と\(3^{2+1}=27\)円が封筒に入れられます。
確認した金額が27円だった場合は、上のような\(n=2\)で金額の高い封筒を確認したか,\(n=3\)で金額の低い封筒を確認したことになります。
考えてみよう
今回の設定なら、お金の入れ方の設定に不備があるようなことはありませんから、堂々と期待値の計算ができます。
そんなわけで、アキラさんは確認した金額を\(3^n\)円としてもう片方の期待値を計算することにしました。
確認した金額が\(3^0=1\)円なら、必ずそれが低い金額なので交換した方が得である。
確認した金額が\(3^n\)円(\(n>0\))なら、それが低い金額である事後確率は\(\frac{1}{3}\)であり、それが高い金額である事後確率は\(\frac{2}{3}\)である。
もう片方の封筒に入っている金額の期待値は\(\frac{1}{3}\times3^{n+1}+\frac{2}{2}\times3^{n-1}=\frac{11}{9}3^n\)円となる。
これは、確認した封筒の金額\(3^n\)円より高いので交換した方が得である。
つまり、確認した金額が何円でも、もう片方の封筒に交換した方が得である!
前回は問題の設定に不備があったせいで、正確な事後確率を使うことすらできずに間違った考えを進めてしまったアキラさんでしたが、今回も考え方は変わりません。
入れられたお金の確率分布がしっかり設定されて、それに応じた事後確率を使って計算したアキラさんの考えに穴はないように見えます。
しかし、カオルさんの考えも変わりません。
最初の封筒の金額を確認するまでは2つの封筒は同じ立場にあるので、交換しても損得はない。
どんな金額を確認しても交換した方がいいという考えは、それが正しいなら確認せずとも交換した方がいいことになるので、正しくない。
つまり、金額を確認しても確認する前と同じように、交換しても損得はない!
(ただし、確実に交換した方が得だとわかる1円を確認した場合は除く)
アキラさんとカオルさんの意見は対立しています。
今回は、問題設定の不備を逃げ道にすることはできません。
どちらが正しいのでしょうか!?
パラドックスの解決
実は、カオルさんの考えに間違いがあります。
このパラドックスを解決するためには、期待値というものがどのような計算でできた値なのかを思い出す必要があります。
期待値は、各事象が起きたときに得られる値にその事象が起きる確率をかけたものの総和で定義されます。
前回のように整備されていない2つの封筒問題では、アキラさんが金額の確認前後の確率を混同してしまったせいで、正確にその事象が起きる事後確率を計算できていませんでした。
ただ、整備されていない2つの封筒問題にはそもそも正しい事後確率など存在せず、ここがパラドックスの原因だったのだと納得して分析を終えていた,もしくは終えるしかなかったのでした。
ところが、今回のように整備された2つの封筒問題では、金額の確認前後の確率をしっかり意識して計算しても、アキラさんとカオルさんの対立が残っています。
つまり、このパラドックスの本質は事後確率の計算の失敗ではなく別の場所にあったのです。
このパラドックスの本質は期待値が総和で定義されているところにあります。
今回の問題で起こり得る事象は種類が無限にあるので、期待値を計算するときに足すべきものも無限にあるわけですが、無限個のものの和については不思議なことが起こります。
例えば、正の整数たち(\(1, 2, 3, \cdots\))と正の偶数たち(\(2, 4, 6, \cdots\))を見てみましょう。
正の整数たちと正の偶数たちを比べてみると、前から何番目の正の偶数も正の整数の2倍の大きさになっています。
では、正の偶数をすべて足した値は正の整数をすべて足した値より大きくなっているでしょうか?
無限個の和を考えるのであれば、答えはどちらも足すと正の無限大で同じになります。
このように無限和を考えるときは、足されていくものに大小関係があっても、足した結果に大小関係がない可能性があるのです。
整備された2つの封筒問題に話を戻すと、アキラさんは正しい計算で「どんな金額を確認した場合でも、交換した方が期待値が大きい」と結論付けました。
これは、「\(3^n\)円を確認して、それが低い金額だった場合と高い金額だった場合」の2つの事象について、賞金と確率の和を計算したものを比べています。
2つの事象ずつを比べれば、\(n\)がどの場合でも交換した方が値が大きいということです。
(確認した金額が1円だった場合だけは、1種類の事象どうしを比べています。)
これに対してカオルさんは、すべて足したものについても大小関係は成り立っていると誤解して、「金額を確認しなくても交換した方が期待値が大きい」に繋がると考えてしまったのです。
これは、すべての事象について、賞金と確率の和を計算したものを比べています。
そして、実際にこのゲームはすべての事象をまとめて期待値を比べると、どちらも正の無限大になっていますから、カオルさんが「金額を確認しなくても交換した方が期待値が大きい」に繋げて矛盾を導いた議論は正しくなかったのです。
この問題に対しては、「どんな金額を確認した場合でも、交換した方が期待値が大きい」という考えが正しい。
無限和では、足されるものに大小関係があっても総和に同じ大小関係があるとは限らないので、上の考えを「金額を確認しなくても交換した方が期待値が大きい」に繋げることはできない。
カオルさんが結論付けた「交換で損得がない」ゲームは、金額を確認できない別のゲームです。
問題で扱っている金額を確認できるゲームは、確認した金額ごとにあり得る状況が再設定されるので、その損得を考察するなら、アキラさんのように「どの金額でも交換が得」とするのが正解です。
言い換えると、金額を確認するまで無限大の期待値があった交換で損得のないゲームが、金額を確認すると有限な期待値で交換が得なゲームたちのどれかに制限されるのです。
最後に
パラドックスに出会ったら、新しくて難しいことを考えるよりも、おなじみで簡単そうで理解していたつもりのことを再確認する方が解決に繋がります。
次回は、この問題から発展した、期待値が引き起こすもっとおかしなパラドックスに触れてみましょう!





お金の入った2つの封筒があり、片方にはもう片方の2倍の金額が入っているが、どちらにいくら入っているかはわからない。
無作為に封筒を1つ選んで中を確認すると1万円が入っていたとき、どちらの封筒を受け取ることが得であるか?