目次
はじめに
てくますプロジェクトのChihiroです!
前回の記事「2つの封筒問題の整備」のパラドックス解決編を更新しました!
まずはそちらを読んでみてください。
整備された2つの封筒問題の解決には無限の不思議さが表れていたわけですが、言われてみればその不思議さも受け入れることができたのではないでしょうか。
しかし、期待値という概念はもっと受け入れ難いパラドックスを引き起こすのです。
本記事は、数学・情報・論理パズルを楽しむ Techmath Project Advent Calendar 2024 の14日目の記事でもあります。
アドベントカレンダーの応援や購読をしていただけると嬉しいです。
2024年3月30日の「第5回すうがく徒のつどい」にて「2つの封筒問題の整備と発展」というタイトルでさせていただいた講演の内容で、Speaker Deckに講演スライド資料を置いています。
2つの封筒問題のおさらい
2つの封筒問題というのは、次のような設定の問題です。
この問題では、「もう片方の封筒の金額の期待値を計算すると10000円より大きくなり、交換すると得である」という意見と、「10000円以外のどんな金額を確認してももう片方の封筒の金額の期待値が高いというのはおかしいので、交換しても損得はない」という意見が対立していました。
しかし、この問題には封筒に入れる金額を決める確率分布が設定されておらず、状況設定に不備があるという解決で終わったのでした。
そこで、封筒に入れる金額を設定しつつ、もともとあった意見の対立を残すように整備した2つの封筒問題を紹介しました。
コインを裏が出るまで投げ続けて、それまでに表が出た回数を\(n\)とする。2つの封筒にそれぞれ\(3^n\)円と\(3^{n+1}\)円が入れられるが、\(n\)の値やどちらにいくら入っているかはわからない。無作為に封筒を1つ選んで中を確認したとき、どちらの封筒を受け取ることが得であるか?
このように問題を整備すると、本質的な原因にたどりつくことができます。
「無限個のものの和を考えるときは、片方の和で足されているものよりももう片方の和で足されているものが常に大きかったとしても、最終的な和どうしを比べるときは大小に差がないかもしれない」という無限の持っている不思議な性質が影響していて、「どんな金額を確認しても交換した方が得」ということが「確認しなくても交換した方が得」に繋がらなくなっていたのです。
得かつ損なゲーム
実は、期待値という概念は、今までの問題たち以上に受け入れ難いパラドックスを生むのです。
はじめにコインを裏が出るまで投げ続け、それまでに表が出た回数を\(n\)とする。
最後にもう1度コインを投げて、表が出たら\(5^n+1\)円獲得し,裏が出たら\(5^n\)円支払う。
このゲームに参加することは得であるか損であるか?
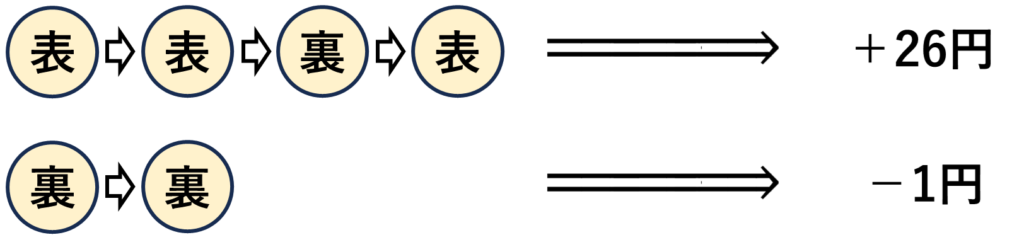
例えば、コインが表→表→裏→表と出た場合は、\(n=2\)で最後が表となるので、\(5^2+1=26\)円獲得できます。
コインが裏→裏と出た場合は、\(n=0\)で最後が裏となるので、\(5^0=1\)円支払うことになります。
考えてみよう
ゲームへの参加の損得を調べるためには、期待値を計算すればいいですね。
そんなわけで、サツキさんはゲームの賞金の期待値を計算することにしました。
表がはじめに\(n\)回出た場合を考えると、お金を獲得する事後確率は\(\frac{1}{2}\)であり、お金を支払う事後確率も\(\frac{1}{2}\)である。
この場合の賞金の期待値は、\(\frac{1}{2}\times(5^n+1)+\frac{1}{2}\times(-5^n)=\frac{1}{2}\)円となる。
表がはじめに何回出ても得なので、このゲームは参加すると得である!
みなさんもこのゲームの賞金を見たとき、獲得するときの金額の方が1円多くなっていることから、細かい計算なしでもサツキさんと同じ結論を得たのではないでしょうか。
サツキさんは、しっかりと計算してそのことを証明したのです。
サツキさんは表がはじめに何回出たかで場合分けして、そのすべてで得することを示したのですが、タクミさんは別の分け方で計算すると異なる結論が得られると考えました。
表が全部で0回出た場合を考えると、必ず1円支払うことになるので損である。
表が全部で\(m\)回(\(m>0\))出た場合を考えると、お金を獲得する事後確率は\(\frac{2}{3}\)であり、お金を支払う事後確率は\(\frac{1}{3}\)である。
この場合の賞金の期待値は、\(\frac{2}{3}\times(5^m+1)+\frac{1}{3}\times(-5^m)=-5^{m-1}+\frac{2}{3}\)円となる。
表が全部で何回出ても損なので、このゲームは参加すると損である!
わざわざややこしく計算したようにも見えますが、計算の流れはサツキさんと変わりません。
サツキさんの計算を認めるのならば、タクミさんの計算も認めなければなりません。
サツキさんとタクミさんの意見は対立しています。
今回は、結論が得と損の真逆に分かれる意見になっていて、2つの封筒問題のようにもなりません。
どちらが正しいのでしょうか?
パラドックスの解決
実は、サツキさんとタクミさんどちらの考えにも間違いがあります。
このパラドックスを解決するためにも、期待値の定義を思い出す必要があります。
期待値は、各事象が起きたときに得られる値にその事象が起きる確率をかけたものの総和でした。
今回も無限個のものの和の性質が原因になっています。
例えば、\(1, -1, 1, -1, 1, -1, \cdots\)のように\(1\)と\(-1\)が交互に無限に並んでいる列を考えてみましょう。
この列の数の総和を計算するとき、\((1+(-1))+(1+(-1))+(1+(-1))+\cdots\)のようにペアを作ってから計算すると、どのペアも和が\(0\)なので、列の数の総和は\(0\)を足し続けていることになり、合計\(0\)になります。
一方で、\(1+(-1+1)+(-1+1)+(-1+1)+\cdots\)のようにはじめの\(1\)だけ残してペアを作ってから計算すると、列の数の総和ははじめの\(1\)に\(0\)を足し続けていることになり、合計\(1\)になります。
このように無限和を考えるときは、足していく順番を変えると計算結果が変わる可能性があるのです。
無限和のときにおかしいことが起きるというよりも、足していく順番を変えても計算結果が変わらないという性質が有限和のときには奇跡的にあった考えた方がいいかもしれません。
得かつ損なゲームに話を戻すと、無限個のものの和である期待値を、サツキさんは表がはじめに\(n\)回出た場合でペアを作って,タクミさんは表が全部で\(m\)回出た場合でペアを作って計算していました。
無限和なのに足していく順番を変えたので、2つの計算結果が違ってもおかしくはなかったのです。
足していく順番が指定されておらず,足していく順番によって計算結果が変わるときには、その無限和の値を考えることはしません。
無限和が足していくと限りなく大きくなるときには、計算結果は数値ではありませんが正の無限大と呼んで扱うこともありますが、そのようなこともできないのです。
今回のゲームは、期待値の無限和が存在しない不思議な状況になっています。
というよりも、無限個のものを足していくという操作をしたにも関わらず、足していく順番を変えても計算結果が変わらないという奇跡的な場合にのみ、その計算結果を無限和として扱うことが許されていたのです。
では、どうやって期待値を求めればよかったのでしょうか?
残念ながら、期待値が上のように定義されている以上は、このゲームに期待値は存在しません。
このゲームに損得勘定の指標が欲しいのであれば、期待値とは違う別のものを用意するしかありません。
このゲームの賞金の期待値は、足していく順番が指定されておらず,足していく順番によって計算結果が変わる無限和だったため、値が存在しない。
得であるという結論も損であるという結論も、それぞれの順番で計算した値を無限和の値だとしたところに誤りがある。
「得かつ損なゲーム」は、得でも損でもない損得勘定の不可能な珍しいゲームだったのです。
(サンクトペテルブルクのパラドックスに出てくるゲームでさえ、期待値は正の無限大という計算結果を持っています)
最後に
賞金と確率が設定されていれば、そのゲームの期待値は必ず存在する……
そう思っていた人も多かったのではないでしょうか。
期待値に頼れなくなったとき、人はこのゲームの損得にどんな印象を抱くのか、とても興味があります。





お金の入った2つの封筒があり、片方にはもう片方の2倍の金額が入っているが、どちらにいくら入っているかはわからない。
無作為に封筒を1つ選んで中を確認すると1万円が入っていたとき、どちらの封筒を受け取ることが得であるか?