創作パズル　パラドックスな子供たち

はじめに

平均って便利ですよね。
平均値は、集団のだいたいの値を私たちに教えてくれます。

成績が良さそうなクラス，年収が高そうな職業，寿命が長そうな国……
個々の値を見なくても判断ができて便利な平均ですが、安易な判断は正しくないかもしれません。

例えば、次のパズルのような状況は本当に起きるのでしょうか？

考えてみよう

問題

年齢が1つずつ違う8人の子供がいます。
眼鏡をかけている子だけを見ると男の子は女の子より平均年齢が1だけ高く、
眼鏡をかけてない子だけを見ても男の子は女の子より平均年齢が1だけ高いのに、
男の子は女の子より平均年齢が1だけ低いそうです。

眼鏡をかけている子がかけてない子より平均年齢が高いとき、
この不思議な子供たちの眼鏡の有無と性別を年上から順に答えてください。

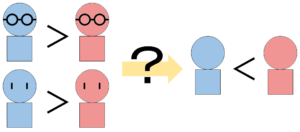
眼鏡をかけていてもかけていなくても男の子の年齢が高いのに、男の子の年齢が低い……？
年齢順に並べる以前に、そもそも矛盾しているのでは？

真相は、解いてみればわかりますよ！

少し下にスクロールすると解答があります。

解答

眼鏡あり女子，眼鏡あり男子，眼鏡あり女子，眼鏡なし男子，眼鏡あり女子，眼鏡なし男子，眼鏡なし女子，眼鏡なし男子

解説

眼鏡をかけた男の子，眼鏡をかけた女の子，眼鏡をかけてない男の子，眼鏡をかけてない女の子は平均年齢を計算できているので、1人ずつはいなければなりません。

平均年齢についての条件しかないので、全員から同じだけの年齢を引いて考えても大丈夫です。
最年少を1歳，最年長を8歳として考えることにします。

男の子の人数を$m$，男の子の合計年齢を$M$とします。
女の子の人数は$8-m$，女の子の合計年齢は$36-M$になり、男の子が女の子より平均年齢が1だけ低いという条件から次の式が成り立ちます。

$$\frac{M}{m}＝\frac{36-M}{8-m}-1$$

$m$が2，3，5，6だとすると、$M$がそれぞれ$\frac{15}{2}$，$\frac{93}{8}$，$\frac{165}{8}$，$\frac{51}{2}$となって自然数でなくなってしまいます。
よって、$m=4$でなければならず、$M=16$となります。

眼鏡をかけた男の子の人数を$m_g$，眼鏡をかけた男の子の合計年齢を$M_g$，眼鏡をかけた女の子の人数を$f_g$，眼鏡をかけた女の子の合計年齢を$F_g$とします。
眼鏡をかけた男の子が眼鏡をかけた女の子より平均年齢が1だけ高いという条件から次の式が成り立ちます。

$$\frac{M_g}{m_g}=\frac{F_g}{f_g}+1$$

眼鏡をかけてない男の子の人数は$4-m_g$，眼鏡をかけてない男の子の合計年齢は$16-M_g$，眼鏡をかけてない女の子の人数は$4-f_g$，眼鏡をかけてない女の子の合計年齢は$20-F_g$となります。
眼鏡をかけてない男の子が眼鏡をかけてない女の子より平均年齢が1だけ高いという条件から次の式が成り立ちます。

$$\frac{16-M_g}{4-m_g}=\frac{20-F_g}{4-f_g}+1$$

自然数解を求めやすいように整理すると、次の式が成り立ちます。

$$(M_g-(m_g+3))(f_g-m_g)=-5{m_g}^2+11m_g$$

$m_g=1$，$M_g=10$，$f_g=2$だとすると、眼鏡をかけた男の子が1人なのに合計10歳になってしまいます。
$m_g=2$，$M_g=7$，$f_g=3$だとすると、$F_g$が$\frac{15}{2}$となって自然数でなくなってしまいます。
$m_g=3$，$M_g=12$，$f_g=1$だとすると、眼鏡をかけた子がかけてない子より平均年齢が低くなってしまいます。
$m_g=3$，$M_g=18$，$f_g=2$だとすると、眼鏡をかけた男の子の合計年齢が男の子の合計年齢を超えてしまいます。

よって、$m_g=1$，$M_g=7$，$f_g=3$でなければならず、$F_g=18$となります。

7歳の子だけが眼鏡をかけた男の子，2歳の子だけが眼鏡をかけてない女の子となり、眼鏡をかけてない男の子3人で合計年齢を9にするには1歳，3歳，5歳の3人でなければならず、残りが眼鏡をかけた女の子となります。
ゆえに、年上から順に眼鏡あり女子，眼鏡あり男子，眼鏡あり女子，眼鏡なし男子，眼鏡あり女子，眼鏡なし男子，眼鏡なし女子，眼鏡なし男子でなければなりません。

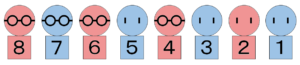
また、この順であれば条件をすべて満たしています。

背景

問題を解くとわかるように、平均の大小が逆転してしまうような状況がありました。
しかし、平均値が嘘をついているわけではありません。
平均をとることで見えなくなった部分が、成り立ちそうな性質を認めてくれないだけです。

平均で見えないもの、それは集団の大きさです。
集団が小さいと他の集団と合わせて考えたときに影響力が小さいので、このパズルのようなことが起こせます。

年齢がとても高い少人数の眼鏡男子で、年齢が高い大人数の眼鏡女子と平均を比べれば男子の方が高くなります。
年齢が低い大人数の眼鏡なし男子で、年齢がとても低い少人数の眼鏡なし女子と平均を比べれば男子の方が高くなります。
そのような集団なら、ほとんどの男子は年齢が低く，ほとんどの女子は年齢が高くなっています。

このような不思議に見える現象は、Simpson(シンプソン)のパラドックスと呼ばれています。
「母集団における相関は、分割した集団における相関とは必ずしも一致しない」ということを言っています。

参考リンク　Wikipedia　シンプソンのパラドックス

この論理パズルは、Simpsonのパラドックスが起きているという条件から具体例を特定するという造りになっています。
条件文に現れる具体的な数字をできる限り減らして、「Simpsonのパラドックスといえばコレ」と言われるパズルを目指しました。