目次
はじめに
てくますプロジェクトでは、てくますゼミと呼ばれる輪読会を隔週で開催しています。
少人数であーだこーだ議論しながら、考える楽しさを分かち合う、ゼミのようなコミュニティです。主に、AIなどの「IT × 数学」領域について学習しています。

現在は「ゼロから作るDeep Learning② 自然言語処理編」という本を読み進めています。
今回は本書第7回の輪読会ということで、7章を読み進めました!
本記事では、今回の勉強会で学んだことをざっくりと紹介していきます。
学習内容
言語モデルの活用
前章で、LSTMを用いて言語モデルを実装してきました。
この章では、実装した言語モデルを活用していきます。
文章生成
言語モデルを用いて、文章生成を行う方法はシンプルです。
言語モデルは、これまで与えた単語から、次に出現する単語の確率分布を出力します。そのため、その確率に応じて、単語を次々と決めていくことで文章生成が可能です。
私も前章で作ったモデルを用いて、youから始まる文章を生成してみました。
you might not be able to get off his position.
but he should avoid economic impact and shock scenario there is a recession.
deficit rises in an apparent signal for the fed to do it.
he said the u.s. funds have spawned an inflation rate of gnp by contrast of some support the rate figures on the economy speed.
in the economic trading reports he recently warned that inflation is going to lead.
意味的な面ではまだまだですが、文構造はある程度しっかりしています。【be able to 動詞】なども使えていて良いですね。
seq2seq
言語データ、音声データ、動画データなどはいずれも時系列データです。
時系列データを別の時系列データに変換したいことがあります。例えば、翻訳や音声認識、質疑応答などです。これらは、入力も出力も時系列データとなります。そのためのモデルとして、seq2seqがあります。
seq2seqはEncoder-Decoderモデルとも言われます。
Encoderで入力の時系列データをLSTMを用いてエンコードし、隠れ状態ベクトルに変換します。そして、そのベクトルをDecoderに引き継ぎます。DecoderはそのベクトルをもとにLSTMを用いて、出力の時系列データを作成します。
seq2seqはEncoderとDecoderの2つのLSTMによって構成されており、その2つの架け橋が、隠れ状態ベクトルであるということですね。
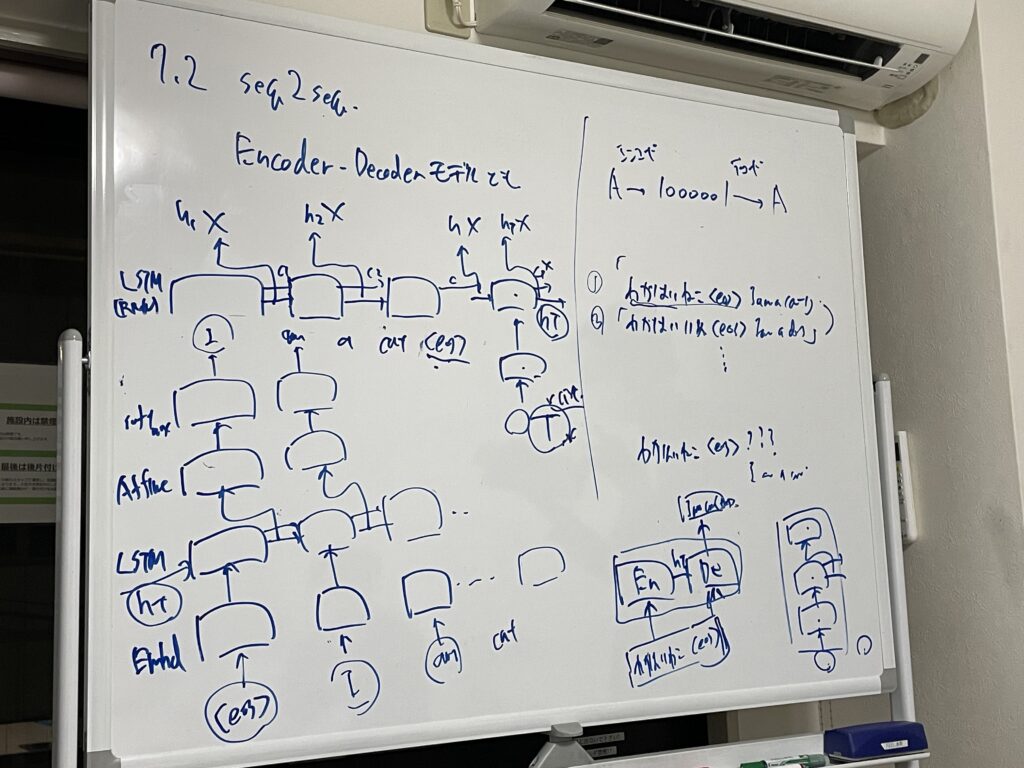
seq2seqの改良
seq2seqのトイプロブレムとして、足し算の問題に取り組みました。

どれも惜しいですが、間違いばかりですね……。
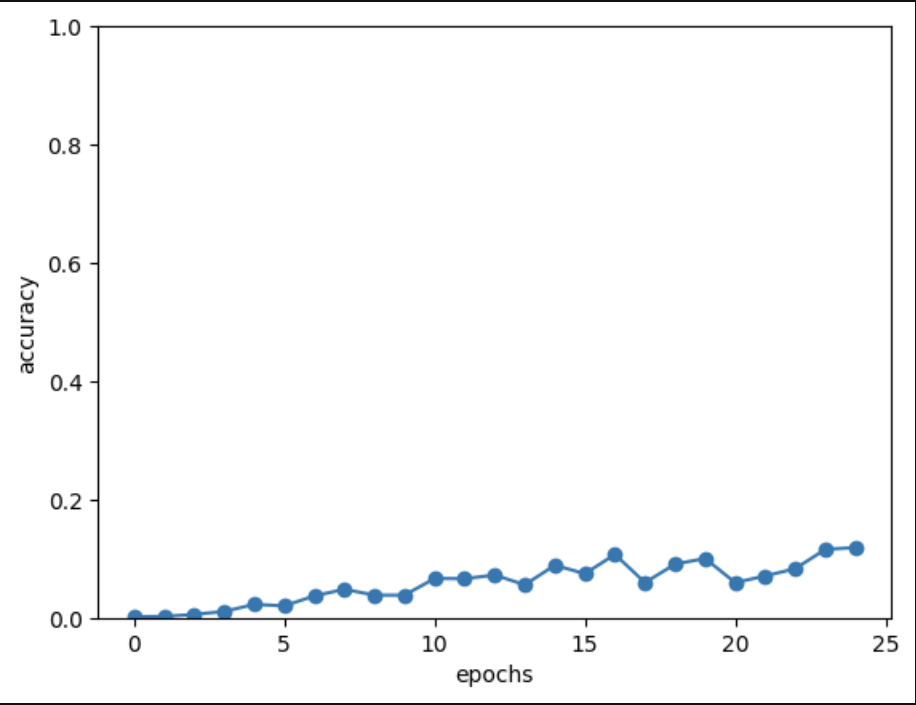
25エポック終了時点で、正解率は11.9%でした。
もっと正解率を上げていきたいですね。モデルを改善していきます。
まず、一つ目の改善点は入力データの反転(Reverse)です。入力の時系列データを反転させるという簡単なトリックで精度が向上します。
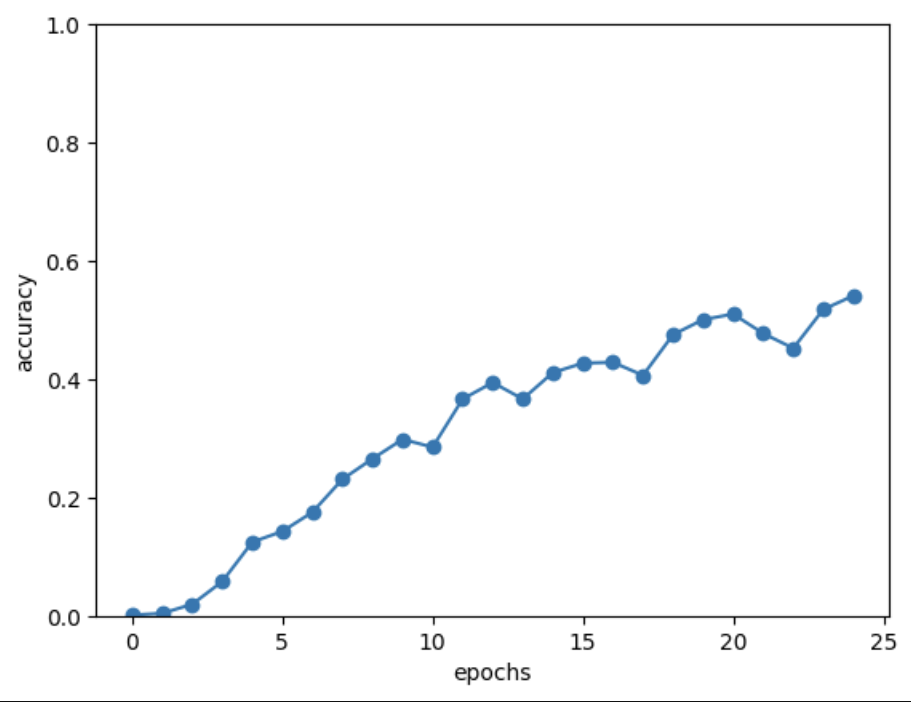
25エポック終了時点で、正解率は54.1%でした。
先ほどより、正解率が上がっています!
なぜ精度が向上するかというと、入力データを反転させることによって、入力データの先頭と出力データの先頭が隣同士になって、勾配がダイレクトに伝わるから、らしいです。このあたりは正直あまり腑に落ちていません。ただ、正解率は確かに上がっていますね!
そして、二つ目の改善点は覗き見の利用(Peeky)です。
これまでの手法では、隠れ状態ベクトルは最初の時刻のLSTMレイヤでのみ用いていました。それをせっかくなので、全ての時刻のLSTMレイヤとAffineレイヤで用いるようにした手法が覗き見です。
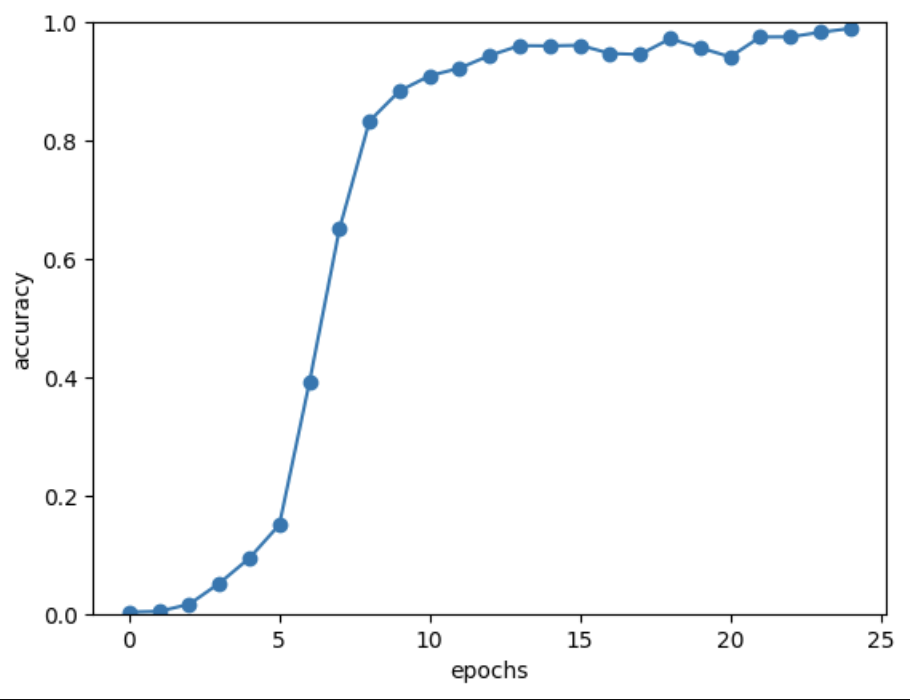
ReverseとPeekyの両方を使うことで、正答率を98.9%まで上げることが出来ました!
最後に
今回は言語モデルの活用として、文章生成や、時系列データから時系列データへの変換を学びました。
自然言語処理で計算問題も学習できるのかな?とは前から思っていたので、今回そのあたりにも触れることができて良かったです。
数字の1ずれがわりと見られたのですが、それは繰り上がりという概念に惑わされているんですかね……?
さて、次回でこの本も最終回。Attentionについて学びます。
では、またね!







