目次
はじめに
てくますプロジェクトでは、てくますゼミと呼ばれる輪読会を隔週で開催しています。
少人数であーだこーだ議論しながら、考える楽しさを分かち合う、ゼミのようなコミュニティです。主に、AIなどの「IT × 数学」領域について学習しています。

現在は「ゼロから作るDeep Learning② 自然言語処理編」という本を読み進めています。
今回は本書第4回の輪読会ということで、4章を読み進めました!
本記事では、今回の勉強会で学んだことをざっくりと紹介していきます。
学習内容
word2vecのボトルネック
前章で作成したシンプルなword2vecでは、巨大なコーパスを扱う際には時間がかかり過ぎてしまいます。
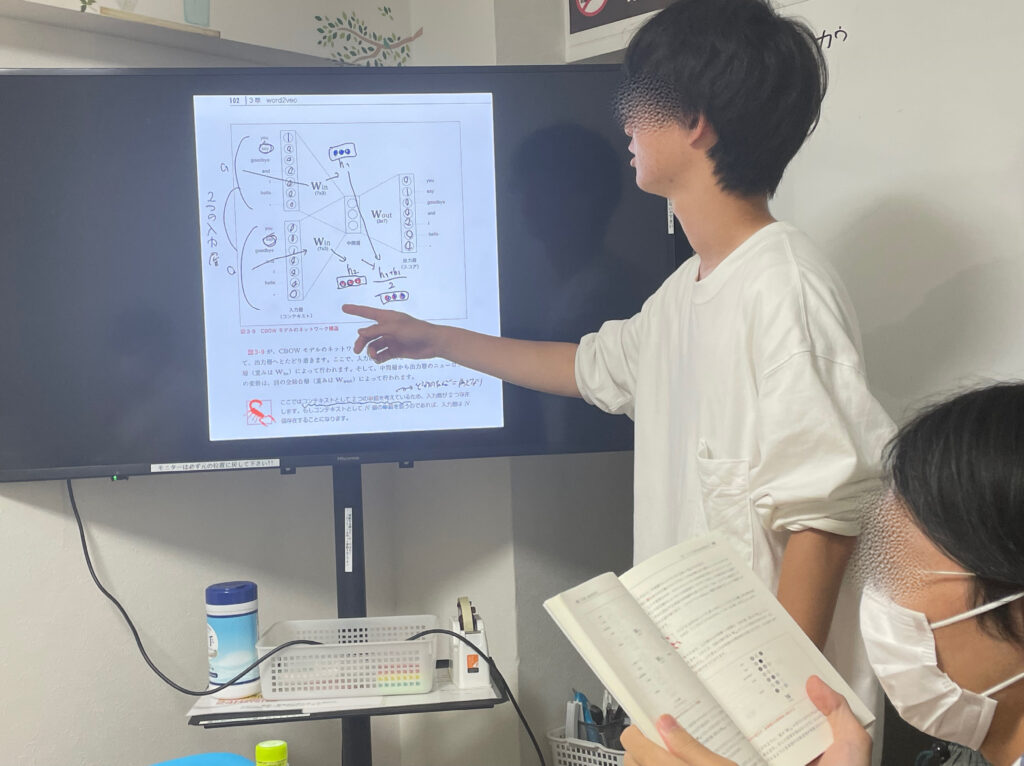
入力層→(W_inと全結合)→中間層→(W_outと全結合)→(ソフトマックス関数)→出力層
上記のうち、ボトルネックになる箇所は次の3点です。
- W_inとの全結合
- W_outとの全結合
- ソフトマックス関数
もう全部じゃんと思いました……笑
これらのボトルネックに対する解決策を本章で学びます。
Embeddingレイヤ
「①W_inとの全結合」ではone-hotベクトルと重み行列W_inの積を計算しています。行列のサイズが大きくなると、この積の計算に時間がかかってしまいます。
しかし、今回はベクトルがone-hotベクトルであるため、行列の積と言いながら、やっていることはW_inの特定行を抜き出しているだけです。
それならば、行列の積の計算をするのをやめて、行列の特定行を抜き出す処理に書きかえましょう。これは簡単に実装できます。
この操作を行うレイヤのことを、Embeddingレイヤと言います。
Negative Sampling
「②W_outとの全結合」「③ソフトマックス関数」のボトルネック解消のキーワードは「多値分類ではなく二値分類で考えよう」です。
CBOWは、文章の前後の単語から中央の単語を考える手法でした。
例: you ? goodbye and i say hello .
前後の you と goodbye から ? に何が入るかを学習/推論します。
? が joy である確率、sayである確率、smileである確率……。
コーパスに100万語ある場合は、? の候補も100万個。
100万個分、? に入る確率を求めなくてはなりません。これは大変です。
そのため、多値分類、すなわちコーパス内の全単語に対して確率を求めることを諦めます。
代わりに考えるのが二値分類です。
? に入るのが say であるか、ないか。
これならただの二択。二値分類です。
二値分類であれば、「②W_outとの全結合」はベクトル同士の内積に抑えられます。「③ソフトマックス関数」の部分はSigmoid関数に置き換えることができます。これによって、ボトルネックを解消するわけですね。
なお、「②W_outとの全結合」は、W_outから特定行を抜き出す処理(Embedding)と、ベクトル同士の内積の計算処理(Dot)の2つをEmbeddingDotレイヤで行います。
二値分類は一つの単語に対して考えるだけでは不十分です。とはいえ、コーパス内の全単語に対して考えるのでは結局また大変です。ですので、適度にサンプリングして考えます。
? に入る正しい単語と、誤りの単語いくつか(5個や10個?)に対し、二値分類を行います。これによって、正例と負例の両方を学習できます。
誤りの単語のサンプリングは、完全ランダムではなく、コーパス内のその単語の出現確率に沿ってサンプリングします。コーパス内に出現しやすい単語ほど、サンプリングされやすいということです。
改良版word2vec
まとめると改良版word2vecは以下のようになります。
入力層→(Embedding)→中間層→(EmbeddingDot)→(Sigmoid関数)→出力層
改良版ができましたので、PTBコーパスという非常に大きいコーパスを使って学習してみました!
改良版とはいえ、私の普通のPCでは、学習がなかなか終わる気配がありませんでした。夜寝て朝起きたら、人知れず終わっていました笑 大体、半日程度かかるらしいです。
巨大なコーパスに対しても学習ができるようになったので進歩ですね!
最後に
前回に引き続き、今回もword2vecについて学びました。次回からはRNNに突入します。
7月は輪読会参加メンバー数名の院試シーズンなので、進めるのは中断。8月からの再開となります。では、またね。







