目次
はじめに
てくますプロジェクトでは、てくますゼミと呼ばれる輪読会を隔週で開催しています。
少人数であーだこーだ議論しながら、考える楽しさを分かち合う、ゼミのようなコミュニティです。主に、AIなどの「IT × 数学」領域について学習しています。

現在は「ゼロから作るDeep Learning② 自然言語処理編」という本を読み進めています。
今回は本書第6回の輪読会ということで、6章を読み進めました!
本記事では、今回の勉強会で学んだことをざっくりと紹介していきます。
学習内容
RNNの問題点
前回のシンプルなRNNレイヤ(エルマンと呼ぶ)では、時間がさかのぼるに従って、勾配消失、または、勾配爆発が起こることがほとんどです。これは、逆伝播の過程で何度も同じ行列がかけられることが原因です。(RNNレイヤでは各時刻で同じ重み行列を使用しているため、同じ行列がかけられます)
1より大きい数値を何度もかけると無限大に発散し、0から1までの数値を何度もかけると0に収束します。これと同様に、行列についても同じものを何度もかけると、その値は指数的に増加、または、減少します。
勾配爆発への対応
勾配爆発への対策は、勾配クリッピングという定番の手法があります。
各勾配をまとめて1つのベクトルとし、そのベクトルのノルムがある閾値以上の場合、そのベクトルの方向はそのままに、大きさを閾値にまで縮めます。
つまり、勾配をまとめたベクトルを \(\vec{v}\) とし、閾値を \(th\) とすると、
\(||\vec{v}|| \geq th\) のとき、 \(th\cdot\displaystyle\frac{\vec{v}}{||\vec{v}||}\) に値を更新するということです。
勾配消失への対応
勾配消失の対策として、「ゲート付きRNN」があります。ゲートとは、ゲートの先に対してデータをどれだけ流すかを制御する仕組みです。
ゲート付きRNNには様々なネットワーク構成があります。この本では、その中でも代表的なLSTMについて取り扱っています。
LSTM
LSTMには忘却ゲート、入力ゲート、出力ゲートがあります。この順にゲートを通っていくことで記憶を管理しています。
- 忘却ゲート
前時刻までの記憶において、何を忘れ、何を覚えておくかを制御する - 入力ゲート
現時刻のどの情報を記憶に加え、どの情報を記憶に加ないかを制御する - 出力ゲート
現時刻の記憶において、その場で利用したい情報を出力用に取得する
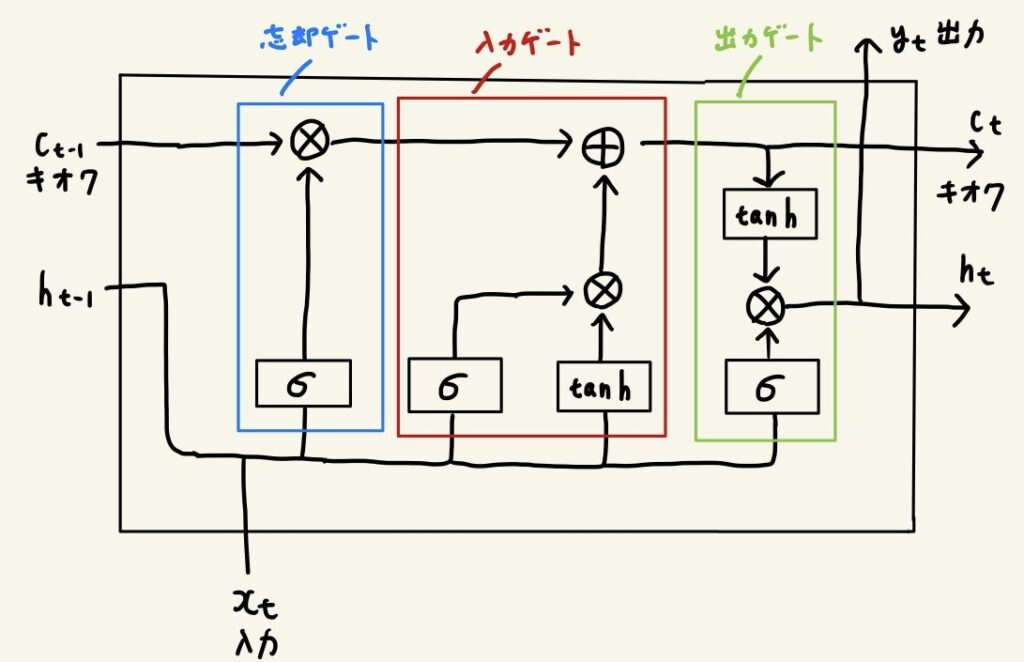
絵がガタガタですみません……笑
乗算は行列としての積ではなく、単に各成分ごとの積です。この積をアダマール積と呼びます。
\(σ\) はシグモイド関数です。
すなわち、 \(σ(x) = \displaystyle\frac{1}{1+e^{-x}}\) です。
シグモイド関数は0〜1の値をとります。この値によって、情報をどの程度流すかを制御します。
\(tanh\) はハイパボリックタンジェント関数です。
すなわち、 \(tanh(x) = \displaystyle\frac{e^x-e^{-x}}{e^x+e^{-x}}\) です。
ハイパボリックタンジェント関数は-1〜1の値を取ります。負の値も取ることが重要で、これによって対義語などの概念を学習することができます。
さて、LSTMではなぜ勾配消失が起きづらいのでしょうか?
\(c_t\) のラインを見ると、登場するのは加算ノードと乗算ノードの2種類のみです。
このうち、加算ノードの逆伝播では勾配の劣化が起きません。
乗算ノード(アダマール積)の逆伝播では、毎時刻異なる値がかけられます。同じ値が繰り返しかけられるわけではないため、勾配消失は起きづらくなっています。
これにより、前回のシンプルなRNNレイヤで起きていた課題を緩和することができました。
最後に
LSTMについて、ネットワーク図を見れば理屈を理解できるものの、機械が「忘却ゲート」「入力ゲート」「出力ゲート」を理解したかのように学習することは驚きです……!
内容がかなり複雑になってきましたね。本ではLSTMのさらなる改善(Dropoutや重み共有など)についても述べられています。ぜひ読んでみてください。
また、今回の内容理解には下記の本が役立ちました。こちらの本も超おすすめなので、ぜひ読んでみてね。
では、また!







