目次
はじめに
てくますプロジェクトでは、てくますゼミと呼ばれる学習会を開催しています。
少人数であーだこーだ議論しながら、考える楽しさを分かち合うことを大切にしています。

現在は「AIエンジニアを目指す人のための機械学習入門」という本を読み進めています。
今回は本書第3回の輪読会ということで、2.6〜2.7を読み進めました!
本記事では、今回の勉強会で学んだことをざっくりと紹介していきます。
学習内容
決定木
決定木は教師あり学習の一つで、ロジスティック回帰やSVCと同様、クラス分類のアルゴリズムです。
特徴量に関する質問(条件判定)をもとにした分岐を繰り返し行い、入力データ分類する手法です。
今回はワインのデータを用いて、ワインの品種を分類します。
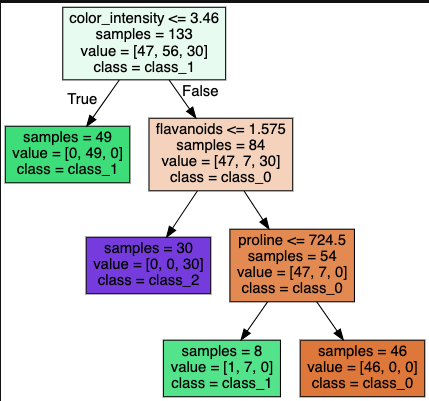
決定木は各ノードに属するサンプルが全て同じクラスになるまで、分割を繰り返します。
ただこれでは過学習に陥りがちなため、木の最大の深さを事前に設定し、その値より深い階層のノードを切り落とすこともあります。これを事前枝刈りといいます。
決定木のメリットはモデルの解釈性が高いことです。以下のように、どの特徴量の重要度が高いかを知ることができます。
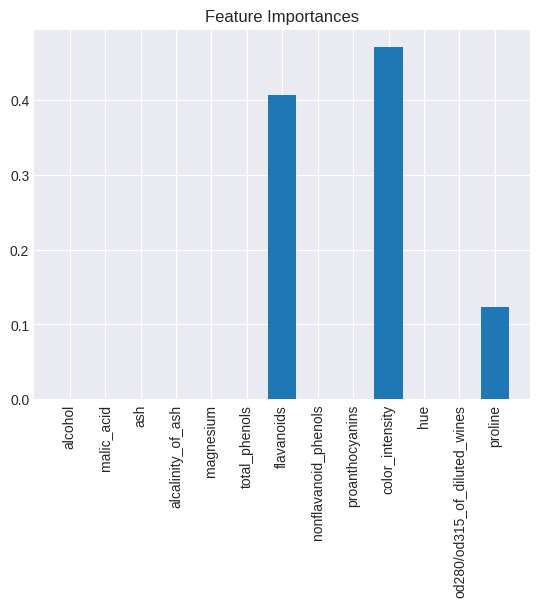
なお、特徴量に関する質問(条件判定)は、情報利得が最大となるように作られます。
情報利得
\(IG(D_p, f)=I(D_p)-\displaystyle\frac{N_{left}}{N_p}I(D_{left})-\displaystyle\frac{N_{right}}{N_p}I(D_{right})\)
\(I\)は不純度を出力する関数、\(D\)はノード、\(N\)はノードのサンプル数を表します。
情報利得を最大にするには、左側と右側の子ノードの不純度を小さくすればよいです。
不純度を出力する関数には、以下の関数がよく用いられます。
- ジニ不純度
\(I_{gini}(t)=\sum_{i=1}^{C}p(i|t)(1-p(i|t))\) - 交差エントロピー誤差
\(I_{entropy}(t)=-\sum_{i=1}^{C}p(i|t)log_2p(i|t)\)
ランダムフォレスト
ランダムフォレストは決定木を複数作成し、各決定木の出力の多数決で分類結果を決める手法です。決定木と比較して、モデルの解釈性は劣りますが、高い性能が出やすいです。
ランダムフォレストは、複数の決定木を組み合わせたアンサンブルモデルです。
アンサンブルにはバギングやブースティングといった手法がありますが、ランダムフォレストはバギングの一種です。
- バギング:並列学習(ランダムフォレストはこっち)
- ブースティング:直列学習
ランダムフォレストでは過学習を防ぐために、2種類のランダム性を取り入れています。
1つ目はデータのランダム性です。複数の決定木において、元データからランダムで復元抽出したデータを学習に使用しています。
2つ目はノード分割に使用する特徴量のランダム性です。ランダムフォレストでは各決定木に全特徴量を使用するのではなく、特徴量の一部をランダムで非復元抽出し、抽出した特徴量のみを使用しています。
2種類のランダム性を取り入れながら、複数の決定木を並列学習させていきます。
最後にデータを分類する際には、複数の決定木に対する予測結果の多数決を取ります。
先ほどと同じワインのデータを、今度はランダムフォレストで学習し、先ほどの決定木よりもテストスコアが高くなることを確かめました!
最後に
今回も前回に引き続き、分類を行うための手法について学習しました。決定木もランダムフォレストも大筋は理解しやすかったですね。
さて、次回はNaive Bayseと主成分分析について学びます。色々なアルゴリズムを頑張って学んでいきますよ〜。
では、また!




