目次
はじめに
てくますプロジェクトでは、てくますゼミと呼ばれる学習会を開催しています。
少人数であーだこーだ議論しながら、考える楽しさを分かち合うことを大切にしています。

現在は「AIエンジニアを目指す人のための機械学習入門」という本を読み進めています。
今回は本書第1回の輪読会ということで、1.1〜2.3を読み進めました!
本記事では、今回の勉強会で学んだことをざっくりと紹介していきます。
学習内容
AIの分類、機械学習の分類
AI(人工知能)は、エキスパートシステムと機械学習システムに分けられます。
- エキスパートシステム
従来のシステムで、人が事前に「もしAならばBする」といったルールをプログラムとして実装するシステムです。 - 機械学習システム
データに潜むパターンをもとに機械(システム)が自らルールを学習するアプローチです。
機械学習は、複雑で大量なルールを人が設定するのは困難であるという課題を解決するためのアプローチとして誕生しました。
機械学習はさらに、教師あり学習、教師なし学習、強化学習の3つに分けられます。
- 教師あり学習
正解付きのデータセットを使って学習し、未知のデータの正解を予測する手法です。主に回帰(数値データの予測)や分類(ラベルデータの予測)といったタスクがあります。 - 教師なし学習
正解の付いていないデータセットから、データの背後にある傾向を学習する手法です。主にクラスタリングや次元圧縮といったタスクがあります。 - 強化学習
試行錯誤を繰り返し、最終的に辿り着きたい状態への最適な行動を学習させる手法です。
主に機器の制御や戦略の構築で役に立ちます。
しばらくは教師あり学習について学んでいきます。
線形回帰
回帰とは入力データを与えたとき、対応する出力データとして、数値データを予測する教師あり学習の手法です。その中でも線形回帰とは、説明変数に対し目的変数が一次式で表されるもののことをいいます。
scikit-learnのlinear_modelを用いて、線形回帰を実装しました。
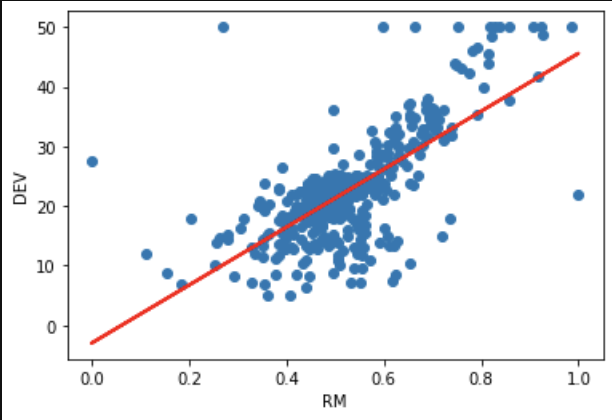
上の図の赤い直線は、各データ点で誤差の2乗をすべて足し合わせた値が最小になるように選んでいます。この考え方を最小二乗法といいます。
(ここで、 \(y_i\) は正解データ、\(\hat{y_i}\) はモデルの予測値です)
L1正則化、L2正則化
教師あり学習では、データを訓練データとテストデータに分割します。
構築したモデルについて、テストデータに対するスコアが訓練データに対するスコアより大きく低下することがあります。これは、モデルが訓練データに対して過剰にフィットしているためです。この現象を過学習と呼びます。
過学習している線形回帰モデルは、訓練データのなるべく多くのデータ点の近くを通ろうとするために、係数の一部の絶対値が大きくなる傾向があります。正則化では、係数に制約をつけることで過学習を防ぎます。
- Ridge回帰(L2正則化)
\(Z = \sum_{i=1}^{n}(y_i – \hat{y_i})^2 + α(ω_0^2+ω_1^2+…+ω_n^2)\) - Lasso回帰(L1正則化)
\(Z = \sum_{i=1}^{n}(y_i – \hat{y_i})^2 + α(|ω_0|+|ω_1|+…+|ω_n|)\)
(\(ω_0, …, ω_n\)は係数です)
これによって実際に、Test Scoreが改善していることを確認しました。
最後に
今回が記念すべき、初のてくますゼミでした。
参加者は2名のみでしたが、ここからコツコツ頑張っていきます!
次回は分類タスクについて学習します。
では、また!












\(Z = \sum_{i=1}^{n}(y_i – \hat{y_i})^2 \) を最小化させる。