目次
はじめに
てくますプロジェクトでは、てくますゼミと呼ばれる輪読会を隔週で開催しています。
少人数であーだこーだ議論しながら、考える楽しさを分かち合う、ゼミのようなコミュニティです。主に、AIなどの「IT × 数学」領域について学習しています。

現在は「ゼロから作るDeep Learning」というディープラーニングの有名な本を読み進めています。
今回は本書第1回の輪読会ということで、2章を読み進めました!
本記事では、今回の勉強会で学んだことをざっくりと紹介していきます。
学習内容(2章)
パーセプトロンとは
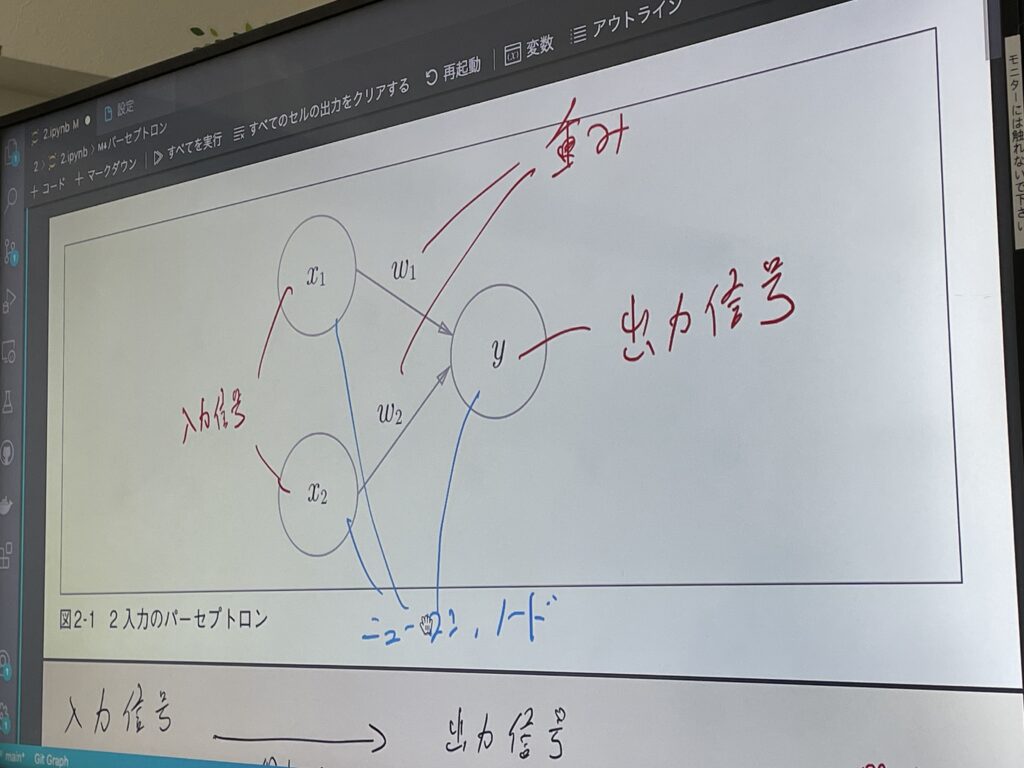
パーセプトロンは、複数の信号を入力として受け取り、1つの信号を出力する関数です。各入力信号を重み付けして足した値が閾値を超えるかどうかで出力信号の値が決まります。
このような単純なモデルでも、適切な重みづけや閾値の設定を行うことで、AND回路、OR回路、NAND回路などが表現できます。
しかし、パーセプトロンではXOR回路を表現できません。XOR回路を実現するためには、単一の層ではなく複数の層を重ねる必要があります。具体的には、NAND回路とOR回路をAND回路でくっつければよいです。
def XOR(x1, x2):
s1 = NAND(x1, x2)
s2 = OR(x1, x2)
y = AND(s1, s2)
return y
print(XOR(0, 0)) # 0
print(XOR(0, 1)) # 1
print(XOR(1, 0)) # 1
print(XOR(1, 1)) # 0とても素朴な例ですが、単一層の限界や、多層にすることによる可能性の広がりを感じられる良い例だと思いました。
論理回路の完備性
輪読会ではテキストの内容から少し脱線して、論理回路の完備性の話で盛り上がりました。「AND回路(∧)、OR回路(∨)、NOT回路(¬)のみですべての論理回路を構成できる」というものです。
例えば、3つの入力信号A, B, Cについて、(1, 1, 0), (1, 0, 1), (0, 1, 1)の場合のみ出力が1になり、それ以外の場合には出力が0になるような論理回路は以下で表現できます。
(A ∧ B ∧ ¬C) ∨ (A ∧ ¬B ∧ C) ∨ (¬A ∧ B ∧ C)
また、NAND回路でAND回路、OR回路、NOT回路を表現できることから、NAND回路だけですべての論理回路を構成できます。
- ¬A = A NAND A
- A ∧ B = ¬(A NAND B)
- A ∨ B = ¬(¬A ∧ ¬B)
このあたりのことは初めて知ったので面白かったです!
最後に
次回はニューラルネットワークの概要について学びます。













