創作パズル　パラドックスなゴムひも

はじめに

この世界の現象は物理学に支配されています。

そんな世界で長く生きている私たちは、状況を聞くとだいたい「どんなことが起こるか」の予想ができます。
木になったリンゴが重くなると枝は下がりそうですし、枝が途中で折れたらリンゴは落ちるか大きく位置が下がりそうです。

ただし、予想がいつも当たるとは限りません。
例えば、次のパズルのような状況は本当に起きるでしょうか？

考えてみよう

問題

太郎くんは一端が天井に結ばれた3mのひものもう一端を掴んでぶらさがっていました。

かかる重さが1kg増える毎に1cm伸びる60cmのゴムが2本あったので、ひもの上下の端に1つずつゴムの端を結び、ゴムのもう一端をそれぞれひもの途中に結んでみました。
太郎くんが再びひもの端を掴んでぶらさがると、30cm高い位置に来るようになりました。

しばらくすると、太郎くんの全体重の負荷に耐えきれず、ひもが1ヶ所切れてしまいました。
しかし、太郎くんは落ちたり下がったりせず、さらに30cm高い位置に来ました。

こんな不思議な体験をした太郎くんの体重を答えてください。
ただし、ひもとゴムの重さや結び目の大きさは無視できるほど小さいとします。

重くてひもが切れたのに、高い位置に移動する……？
体重を計算する以前に、そもそも矛盾しているのでは？

真相は、解いてみればわかりますよ！

少し下にスクロールすると解答があります。

解答

70kg

解説

太郎くんの体重を$m$kgとします。
ひもの上端に端を結んだゴムをゴムAとして、ゴムAのもう一端はひもの下から$a$cmのところに結んだとします。
ひもの下端に端を結んだゴムをゴムBとして、ゴムBのもう一端はひもの上から$b$cmのところに結んだとします。

$a+b>300$ではないことが、ひもが切れたときの結果からわかります。
$a+b>300$だとすると、下から$a$cmまでの部分や上から$b$cmまでの部分が切れたときには太郎くんが上がることはなく、それ以外の部分が切れたときには太郎くんが落ちてしまうからです。
つまり、図の左のように結ばれています。

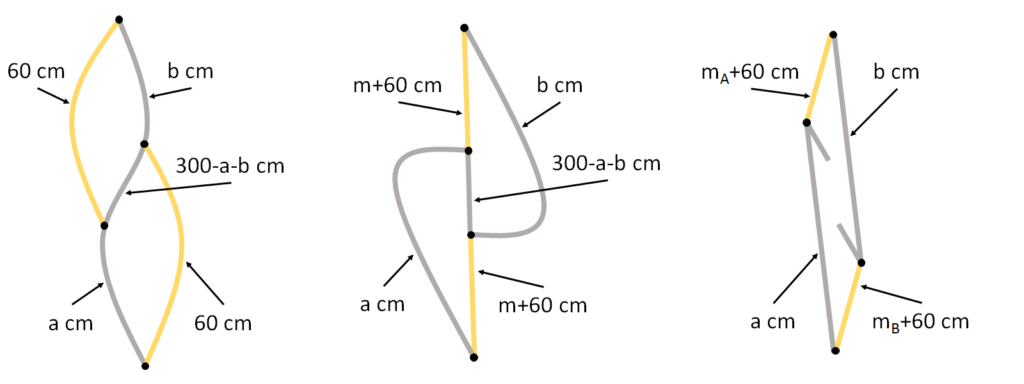
ゴムを結んだ後に太郎くんがぶらさがると30cm高い位置に移動しました。
ひもの下から$a$cmまでの部分がたるんでいるための条件は次で表されます。…①

$$(m+60)+(300-a-b)<a$$

この条件が満たされていることが、ひもが切れたときの結果からわかります。
この条件が満たされていないとすると、下から$a$cmまでの部分や上から$b$cmまでの部分が切れたときには太郎くんが上がることはなく、それ以外の部分が切れたときには全体重の負荷によるものではないからです。

同様に、ひもの上から$b$cmまでの部分がたるんでいることがわかり、その条件は次で表されます。…②

$$(m+60)+(300-a-b)<b$$

①と②の条件のもと太郎くんが天井から270cmの位置にくるための条件は次で表されます。…③

$$2(m+60)+(300-a-b)=270$$

これらは、図の中央のようになっています。

ひもが切れた後に太郎くんはさらに30cm高い位置に移動しました。
下から$a$cmまでの部分や上から$b$cmまでの部分が切れたときには太郎くんが上がることはないので、切れた場所はそれ以外の部分でなければなりません。

このとき、太郎くんを吊るものは2つの部分に分かれています。
ゴムAの含まれている側が太郎くんの体重の$m_A$kgの負荷を担っていて、ゴムBの含まれている側が太郎くんの体重の$m_B$kgの負荷を担っているとすると、太郎くんが天井から240cmの位置にくるための条件は次で表されます。…④

$$(m_A+60)+a=(m_B+60)+b=240$$

$m_A+m_B=m$なので、④が成り立つためには次の条件を満たす必要があります。…⑤

$$m+120+a+b=480$$

これらは、図の右のようになっています。

③と⑤を$m$と$a+b$に関する連立方程式として解くことで、$m=70$，$a+b=290$でなければならないとわかります。

また、例えば$m=70$，$a=145$，$b=145$のとき、条件をすべて満たします。

背景

問題を解くとわかるように、途中のひもが切れたのに高い位置に移動してしまうような状況がありました。
ひもが切れたと聞くと、切れたひもの下側が下がってしまうという事実から、太郎くんの位置も下がると思ってしまいがちです。
しかし実際は、切れたひもの下側より下にあったゴムBが担う体重が小さくなったことにより縮む影響の方が大きいので、太郎くんの位置は上がるのです。

このような不思議に見える現象は、Braess(ブライス)のパラドックスと呼ばれています。
交通工学において「交通網に新たな道を作ることで、移動時間が増加する場合がある」ということを言っています。

参考リンク　Wikipedia　ブライスのパラドックス

ブライスのパラドックスはこのパズルのようにゴムやばねを使った実験として紹介されることもあります。
体重が交通網の利用者数，ひもが利用者数によらず固定の時間がかかる道，ゴムが利用者数によって所要時間が変わる道に対応しています。
実際の道も利用者数によって渋滞が起こり所要時間が変わりますが、より理想的なふるまいをするゴムやばねをパズルの題材にしました。

この論理パズルは、Braessのパラドックスが起きているという条件から具体例を特定するという造りになっています。
条件文に現れる量を単純な値にすることで、「Braessのパラドックスといえばコレ」と言われるパズルを目指しました。