目次
はじめに
現実世界において、嘘つきは多弁であることが多いですが、論理パズルの世界においては、嘘つきが多弁だと扱いに困ります。
たくさんの嘘をすべて正しい命題に変えていくのも大変なのですが、どのように正しい命題に変えていくべきなのかもわかりにくいからです。
発言のうち何が嘘になるべきなのかイメージしてから、問題を解いてみてください。
考えてみよう
問題
太郎さんは次郎さんに4つほど情報を出したように見えますが、嘘は何回ついたのでしょうか?
少し下にスクロールすると解答があります。
解答
4
太郎さんの長い発言は2つの命題からなり、以前には「素数である。」と話している。
(太郎さんの長い発言を1つの命題からなるとみなすと解答が8に,
3つの命題からなるとみなすと解答が2に変わります。)
解説
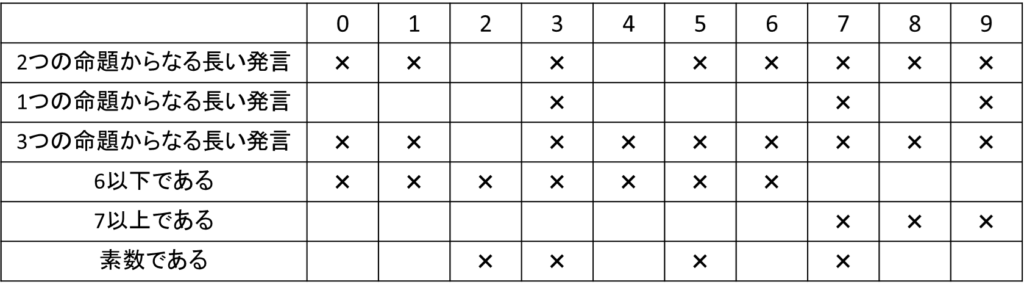
太郎さんの発言「偶数ではない。4の約数ではなく、10の約数ではない。」は句点で分けられた2つの命題になっています。
太郎さんの話す命題はすべて偽なので、「偶数である」と「4か10の約数である」という情報が次郎さんに追加され、次郎さんには2か4であることがわかります。
以前の発言が「6以下である。」ならば、「7以上である」という情報になるので、矛盾が発生します。
以前の発言が「7以上である。」ならば、「6以下である」という情報になるので、次郎さんは数字を特定できません。
以前の発言が「素数である。」ならば、「素数ではない」という情報になるので、次郎さんは数字が4だと特定できます。
この問題は、太郎さんの発言をいくつの命題からなるとするかによって、たどり着く解答が変化します。
「偶数ではない。4の約数ではなく、10の約数ではない。」を1つの命題だとみなしてしまうと、次郎さんには「4か10の約数か偶数である」という情報が追加されたことになり、
以前の発言が「6以下である。」のときだけ、次郎さんは数字が8だと特定できます。
「偶数ではない。4の約数ではなく、10の約数ではない。」を3つの命題だとみなしてしまうと、次郎さんには「偶数である」と「4の約数である」と「10の約数である」という情報が追加されたことになり、
以前の発言が「7以上である。」のときだけ、次郎さんは数字が2だと特定できます。
背景
正直者の発言は、そのまますべて信用して推理に使えばいいので単純です。
しかし、嘘つきの発言には、否定にしなければならない面倒さだけではない複雑さがあります。
部分否定するか全否定するかの複雑さです。
句点があるのに命題が繋がっていると考えてしまうと、太郎さんの長い発言を1つの命題からみなすことになり、否定するべき情報を部分的にしか否定できないことになります。
読点しかないのに命題が切れていると考えてしまうと、太郎さんの長い発言を3つの命題とみなすことになり、否定してはいけない情報も全否定してしまうことになります。
この問題は、命題としての区切り方に対して、それぞれ別の解答にたどり着くようになっています。
最後に
嘘を扱うなら、命題の切れ目を明確に定義する必要があるのは当然です。
文頭に「さらに、」とかを持ってくる嘘つきはもう知りません!
この記事もオススメ
嘘とは何か?に迫るパズルはこちら。










常に嘘をつくことで知られている太郎さんは、0~9のうち太郎さんが好きな数字1つについて、次郎さんに次のように話しました。
「偶数ではない。4の約数ではなく、10の約数ではない。」
太郎さんの好きな数字について太郎さんから「6以下である。」,「7以上である。」,「素数である。」という発言のうちどれか1つだけ以前に聞いていた次郎さんは、太郎さんの好きな数字がわかりました。
太郎さんの好きな数字は何でしょうか?