輪読会「ゼロから作るDeep Learning」第２回

はじめに

てくますプロジェクトでは、てくますゼミと呼ばれる輪読会を隔週で開催しています。

少人数であーだこーだ議論しながら、考える楽しさを分かち合う、ゼミのようなコミュニティです。主に、AIなどの「IT × 数学」領域について学習しています。

てくますゼミ（Connpass）

現在は「ゼロから作るDeep Learning」というディープラーニングの有名な本を読み進めています。

リンク

今回は本書第２回の輪読会ということで、３章を読み進めました！

本記事では、今回の勉強会で学んだことをざっくりと紹介していきます。

学習内容（３章）

ニューラルネットワークとは

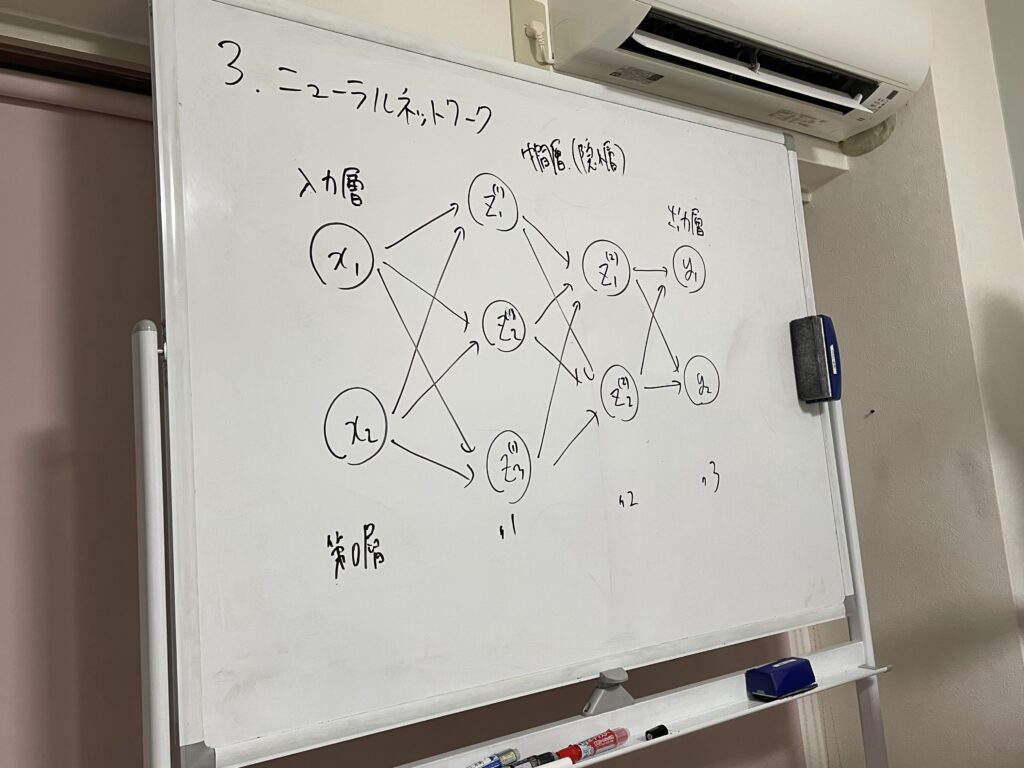
ニューラルネットワークは、ニューロンのつながり方に関しては、パーセプトロンと同じです。

ただし、パーセプトロンでは活性化関数にステップ関数を用いるのに対し、ニューラルネットワークではシグモイド関数などの様々な活性化関数を用います。

ニューラルネットワークにおいて、第n層から第n+1層への処理は次の２ステップです。
１．重み付き入力信号とバイアスの総和を計算
２．活性化関数による変換

活性化関数は非線形関数にすることがポイントです。線形関数は多層にしても線形関数の域を抜け出せないためです。活性化関数の例として、ステップ関数、シグモイド関数、Relu関数、ソフトマックス関数を取り扱いました。当然すべて非線形関数です。

ニューラルネットワークの推論処理

ニューラルネットワークの推論処理とは、学習した重みパラメータやバイアスパラメータを使って、入力値から出力値を求めることを言います。その計算式は行列の積を用いてシンプルに表現できます。

def predict(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']
    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, W3) + b3
    y = softmax(a3)
    
    return y

この章では、推論の具体例として、MNISTのデータセットを用いて、0〜9の手書き数字認識を取り扱いました。ただし、既にモデルは学習済みであることを前提とし、推論部分のみの実装としました。与えられた学習済みモデルの精度は93.52%でした。