目次
はじめに
メイクテンやテンパズルと呼ばれるパズルをご存じでしょうか?
与えられた数字4つに対して、四則演算の記号3つと必要ならばいくつかの括弧をあわせて一列に並べ、計算結果が10になるようにするパズルです。
例えば、2,3,3,7が与えられた場合は、2×3+7-3と計算すれば10になるので正解です。
また、この問題なら7+(3+3)÷2と計算しても10になるので正解です。
32÷3+7や(23+7)÷3のように計算してはいけません。
今回紹介するのは、一味違う見た目のメイクテンのパズルです。
計算パズルが得意な人にはもちろん考えてほしい一問ですし、そうでない人にもメイクテンの世界を俯瞰できるこの問題はオススメです。
考えてみよう
問題
使う数字を決めないってことは、どんな数字で計算してもいいってこと??
どんなメイクテンなのか全く情報がないのでは?
いいえ、このメイクテンは”別解がないこと”がわかっているメイクテンです。
少し下にスクロールすると解答があります。
解答
8÷(1-1÷5)
解説
4つの数字の組すべてを探索し、それぞれについて式の作り方をすべて探索することで、解答にたどりつくことはできます。
しかし、できるだけ論理的に解けるように当たりを付けてみましょう。
○や△や□で、2や3のような数字や,4×2や(5-3)のような式のかたまりを表すとします。
まず、+は解答に使われていないと推測することができます。
○+△が解答の式に現れるとしたら、その部分を△+○に置き換えた式が別解になるからです。
ただし、○と△が同じ数字や式の場合は+が解答に使われている可能性は残ります。
同様に、×は解答に使われていないと推測することができます。
○×△が解答の式に現れるとしたら、その部分を△×○に置き換えた式が別解になるからです。
ただし、○と△が同じ数字や式の場合は×が解答に使われている可能性は残ります。
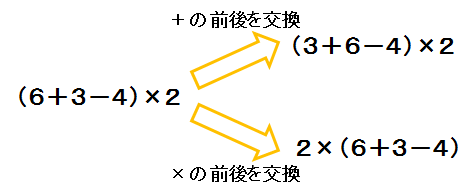

(3×3+4÷4のような別解はある。)
残った-と÷は基本的に値が減る演算なのですが、これらだけで10を作るとなると特別な状況でなければなりません。
引く数が負の数になっていれば-で値は増えますが、その部分は-(○-△)の形になっているので、その部分を-○+△に置き換えた式が別解になります。
よって、解答では-で値を増やすことができません。
割る数が分数になっていれば÷で値が増えることがあります。
ただし、その部分が÷(○÷△)の形になっていると、その部分を÷○×△に置き換えた式が別解になります。
よって、÷(○÷△-□)や÷(□-○÷△)の形になっていなければなりません。
ゆえに、解答はW÷(X÷Y-Z)かW÷(Z-X÷Y)のアルファベットに数字を充てた形をしていると推測できます。
W×Yが10の倍数になっていることなどから、解答に使われている4つの数字の組の候補を絞ることができます。
その中で、別解なく10を作ることができるのは1,1,5,8の組であり、8÷(1-1÷5)=10となります。
背景
メイクテンの世界では、1,1,5,8で10を作る問題が難しいと有名です。
その理由としては、主に次の2つが考えられます。
- 直感に反する途中経過がある。
今回出てきた8÷(1-1÷5)は途中経過に分数で割るという動作が必要です。
他にも(9×9+9)÷9のように、途中経過にとても大きな数が現れる問題も難しい印象を与えます。 - 別解が少ない。
(9×9+9)÷9が解答になる問題は、計算結果を10にする方針がこれしかなく、この式か(9+9×9)÷9を見つけなければ正解できません。
パズルが別解を持つべきでないという観点で見れば、メイクテンには実質1種類しか問題がないということがわかります!
1,1,5,8の問題が難しいことはよく語られますが、このように特別な問題であることはあまり語られていません。
今回は、具体的に1つのメイクテンを解いてもらう問題ではなく、「メイクテンを解くこと」について考えてもらう問題を扱いました。
このようなパズルをメタパズルと呼びます。
最後に
この世のメイクテンすべてを解いたような気分になれてお得でしたね!
「何もないパズル」シリーズはいくつかあるので、他も楽しみにしていてください。
この記事もオススメ
「何もないパズル」シリーズはこちら。












あるメイクテンを解いてください。
そのメイクテンには別解はないです。
そのメイクテンで使う4つの数字は教えないです。