創作パズル　何もない虫食い算

はじめに

虫食い算という計算パズルはご存知でしょうか？
いくつかの数字が虫食いで消えてしまっている筆算の式を復元するパズルです。

たとえば、図の左にある虫食いされた式は右のように復元されます。

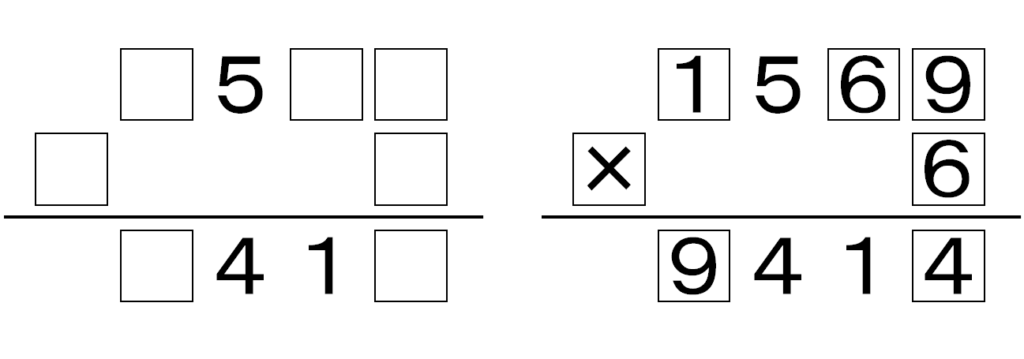
虫食い算はパズルとして解く楽しみだけでなく、式の形や残った数字を見て楽しむ芸術としての要素も持っています。

例題の虫食い算は掛け算であるということまで推理しなければならない変わり者でしたが、この記事ではもっと変な虫食い算を紹介しようと思います。

考えてみよう

問題

一の位が0ではない2桁の数どうしを掛けて3桁の数を計算した筆算を虫食いにしました。
元の掛け算の式を答えてください。
残っている数字が1つしかないですが、別解はないです。
普通の虫食い算は穴のあいた筆算を見せますが、省略します。

残っている数字も、教えてくれなきゃ残っていないのと同じでしょ……
どんな虫食い算なのか全く情報がないのでは？

いいえ、この虫食い算は”別解がないこと”がわかっている虫食い算です。

少し下にスクロールすると解答があります。

解答

12×79=948
残っていた数字は掛ける数の十の位の7

解説

筆算で数字が書かれる場所を図のように①～⑫で示すことにします。
⑤は筆算の途中式の桁の大きさによって、枠があるかどうか変わります。
⑥(枠⑤があるとき)，⑦，⑨，⑪，⑫，以外には0は入りません。

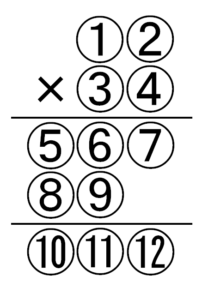
まず、枠⑤のない筆算を考えます。

①に9が入るとすると、①②×③④は最小でも91×11になり計算結果が3桁になりません。
よって、①には9は入りません。

同様に③に9が入るとすると、①②×③④は最小でも11×91になり計算結果が3桁になりません。
よって、⑨にも9は入りません。

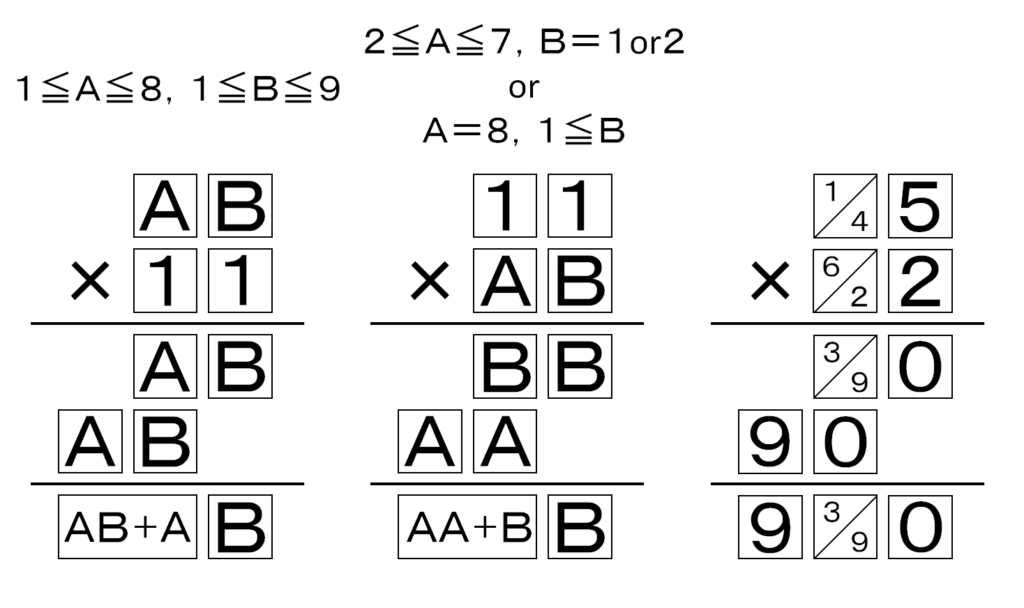
ここで、ＡＢ×11(1≦Ａ≦8，1≦Ｂ≦9)，11×ＡＢ((2≦Ａ≦7，Ｂ＝1か2)または(Ａ＝8，1≦Ｂ)，15×62，45×22の筆算を考えると、すべての場所で，入り得るすべての数字が2回以上現れることがわかります。
よって、問題の虫食い算が枠⑤のない筆算から数字1つだけ残したものだった場合は別解が存在してしまいます。

次に、枠⑤のある筆算を考えます。

枠⑤がない筆算での考察と同様に、①と③には9は入りません。

④に1が入るとすると、①②×④が最大でも99×1になり途中式が3桁になりません。
よって、④に1は入りません。

⑤に5以上の数字が入るとすると、繰り上がりを考慮しても①×④で41以上ないといけません。
そのためには①が5以上でなければならず、⑧には①×③以上である5以上の数字が入ります。
すると、⑤＋⑧が10以上になり計算結果が3桁になりません。
よって、⑤には5以上の数字は入りません。

⑧に9が入るとすると、⑤＋⑧が10以上になり計算結果が3桁になりません。
よって、⑧には9は入りません。

③に8が入るとすると、⑧が9にならないように①②＝11でなければいけません。
すると、①②×③が最大でも11×9になり途中式が3桁になりません。
よって、③には8は入りません。

⑩には①＋⑧以上である数字が入るので、1は入りません。

ここで、ＡＢ×19(Ａ＝1か2，4≦Ｂ)，Ａ1×1Ｂ((Ａ＝3か5，4≦Ｂ)または(Ａ＝5か6，Ｂ＝2か3))，12×Ａ9と21×Ａ5と22×Ａ5(1≦Ａ≦4)，75×1Ａ(Ａ＝2か3)，49×1Ａ(Ａ＝4か6)，14×ＡＢ(Ａ＝5か6，Ｂ＝8か9)，13×19，81×12，83×12の筆算を考えると、③に7が入るかどうかを除き、すべての場所で，入り得るすべての数字が2回以上現れることがわかります。
よって、問題の虫食い算が枠⑤のある筆算から数字1つだけ残したものだった場合は、③に7が書かれている問題を除き、別解が存在してしまいます。

枠⑤があり③に7が書かれているだけの虫食い算を考えてみましょう。

①②×7は⑤⑥⑦と足し合わせて3桁でなければならないので89以下である必要があり、①②＝11か12となります。
①②×④が100以上でなければならないので、①②＝12，④＝9でなければなりません。

また、12×79は枠⑤があり3桁の数を計算する筆算になっています。