創作パズル　何もないジグソーパズル

はじめに

ジグソーパズルはお好きですか？
ジグソーパズルは物理的なパズルですが、この記事では論理パズルとして楽しむことができます。

それでは、問題を解いてみましょう！

考えてみよう

問題

次の3×4のジグソーパズルの完成図を答えてください。

ピースには絵がなくて裏表の区別もないです。
各ピースは1つ以上の辺が凹部か凸部になっていますが、すべての凹部，凸部は同じ形をしていて区別がないです。
同じ形のピースはなく、回転や反転を除いて別解はないです。
回転や反転による別解もなくなるように、左上のピースだけ図のように固定しました。

しかし、他のピースは失くしてしまいました。

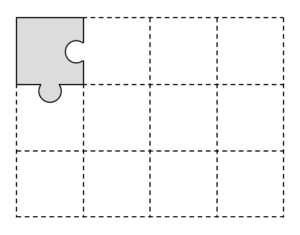
絵も裏表も凹凸の差もないジグソーパズル？？
ピースすら見れないなんて、どんなジグソーパズルなのか全く情報がないのでは？

いいえ、このジグソーパズルは”別解がないこと”がわかっているジグソーパズルです。

少し下にスクロールすると解答があります。

解答

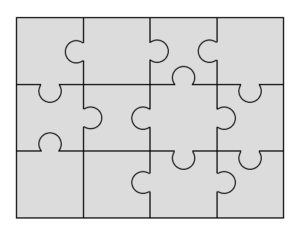
解説

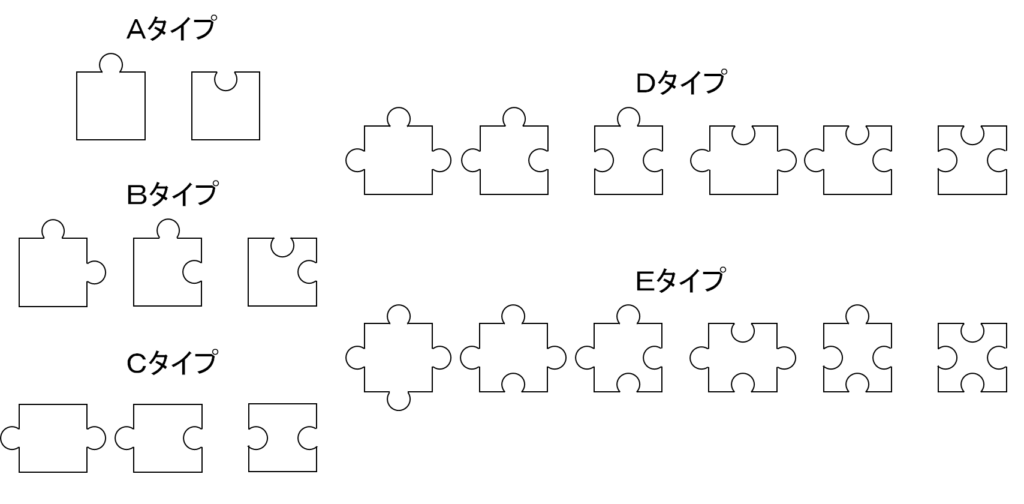
凹凸1つのピースをＡタイプ，隣接した凹凸2つのピースをＢタイプ，離れた凹凸2つのピースをＣタイプ，凹凸3つのピースをＤタイプ，凹凸4つのピースをＥタイプと呼ぶことにします。

左上に固定された凸と凹のＢタイプピースも一旦盤から外して考えることで、回転，反転させた盤面を同一視してケースを列挙できるようにします。

盤には角が4つありますが、角を埋められるＢタイプは3種類しかありません。
Ａタイプを1つだけ盤の角に置いても、別の角が生まれてしまいます。
Ａタイプは図のように組み合わせて使うことではじめて角を1つ埋めることができます。

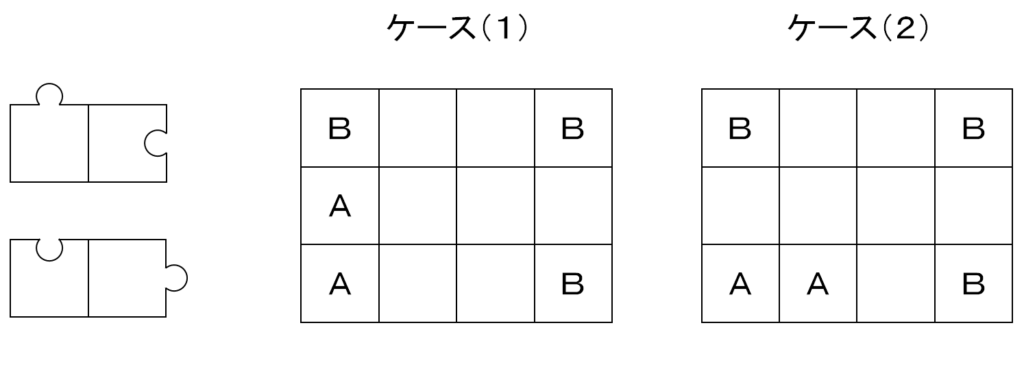
ここで、問題の解をとりあえず1つ見つけるために、使用するピースセットに次の仮定を与えて、できるだけジグソーの別解が生まれないようにしようと思います。

仮定

全体で1つ以下しか使えないＥタイプを1つ採用して，そうすることで2つ以下しか使えなくなるＣタイプを2つ採用します。
さらに、Ｅタイプピースに回転の余地を残すと解の可能性が増えそうなので、すべて凸かすべて凹なＥタイプピースを採用します。

ケース(１)にＥタイプが使われていると、残りがすべてＤタイプでなければいけなくなり、Ｃタイプを使用することに反します。
よって、ケース(１)ではないとわかります。

すべて凸なＥタイプピースを採用した場合を考えます。
平らな辺の向かいが凹なＤタイプは3種類しかないので、①は右に凸でなければいけません。

(ⅰ)②が上に凸な場合を考えます。
凸なＡタイプピースは1種類しかないので、③は左に凸でなければいけません。
Ｌ1で切った右のかたまりを上下反転した形が別解にならないように、④は右に凸でなければいけません。
Ｌ2で切った右のかたまりを上下反転した形が別解にならず，使用するＤタイプに被りがないようにするために、⑤は右，⑥は左に凸でなければいけません。
使用するＢタイプ，Ｄタイプに被りがないようにするために、⑦と⑧は下に凸でなければいけません。
使用するＢタイプに被りがないようにするために、⑨と⑩は左と下か，右と上に凸でなければいけません。

(ⅱ)②が下に凸な場合も同様に考えると、③～⑩はケース(ⅰ)の逆向きになります。
使用するＢタイプ，Ｃタイプに被りがないようにするために、⑨と⑩は左と下に凸でなければいけません。

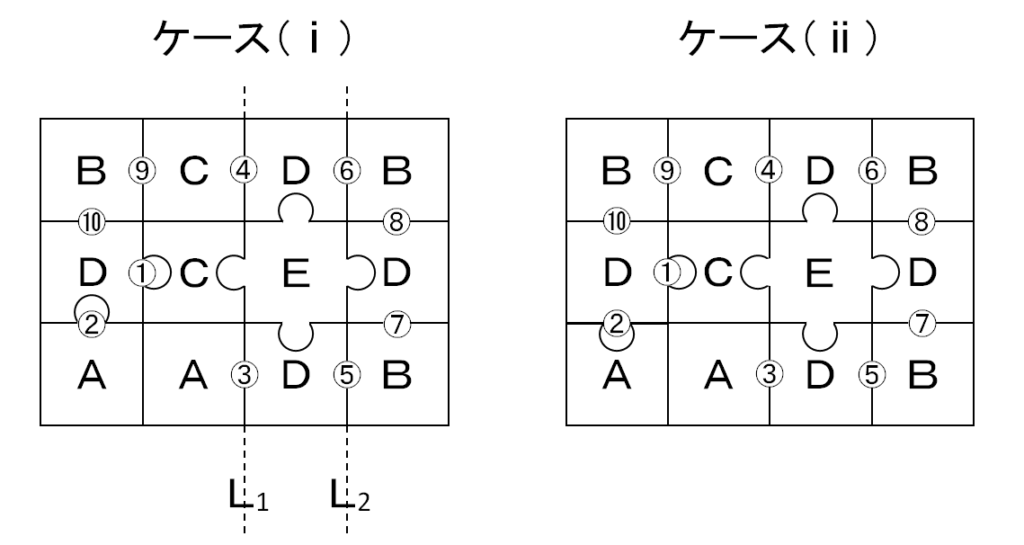
ケース(ⅰ)で⑨と⑩が右と上に凸な場合とケース(ⅱ)で⑨と⑩が左と下に凸な場合は、使用するピースセットが同じなので互いに別解になってしまいます。
よって、すべて凸なＥタイプピースを採用した場合は、ケース(ⅰ)で⑨と⑩が左と下に凸な場合だけそのピースセットで別解を作れないとわかります。
左上のピースを固定された通りになるように回転，反転した完成図がこの問題の解答の1つとなります。

また、すべて凹なＥタイプピースを採用した場合を考えると、同様に1種類のピースセットだけ別解がないと言えるのですが、左上のピースを固定された通りになるように回転，反転することができず、この問題の解答にはなりません。