創作パズル　何もない覆面算

はじめに

覆面算という計算パズルはご存知でしょうか？
数字が文字に置き換わっている等式を見て、もとの式を推理するパズルです。
ただし、同じ数字は同じ文字に，違う数字は違う文字に置き換わっています。

図の左側にある文字列は四則演算記号や等号も覆面になった式で、右側の等式がその解答のうちの1つになります。

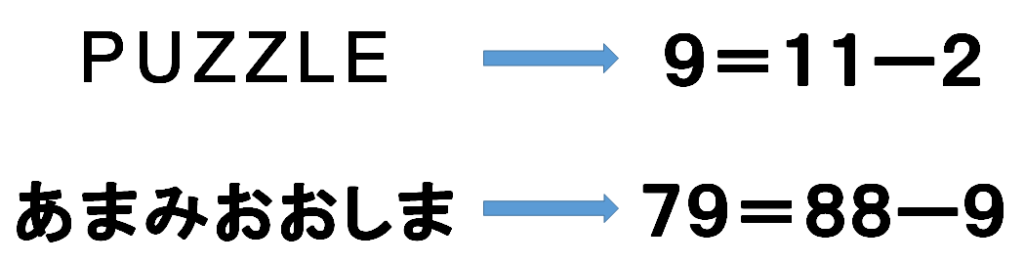
覆面算はパズルとして解く楽しみだけでなく、覆面になった文字列を見て楽しむ芸術としての要素も持っています。
例題の覆面算は記号も覆面になっている変わり者でしたが、この記事ではもっと変な覆面算を紹介しようと思います。

考えてみよう

問題

覆面にされた等式を答えてください。
＋，－，×，÷，＝もあれば全て覆面にしたので、1列に並んだ文字だけになっています。
普通の覆面算のように、0は2桁以上の数の最高位には来ず、－0という表記もしません。
別解はなく、その中で一番短い文字列の覆面算です。
普通の覆面算は文字列を見せますが、省略します。

どれが計算記号かもわからない，覆面の式もわからない……
どんな覆面算なのか全く情報がないのでは？

いいえ、この覆面算は”別解がないこと”がわかっている最小の覆面算です。

少し下にスクロールすると解答があります。

解答

9＋1＝10

解説

もとの式には等号が含まれていて、左右の計算された数の間にあるはずなので、覆面の式は3文字以上から成ります。

覆面の式が3文字の場合
等号は2文字目になり、1文字目に対応する数と3文字目に対応する数が等しいという式が解になります。
その覆面算は「ABA」の形をしていて、「1＝1」と「2＝2」が解になるので、別解を持ってしまいます。

覆面の式が4文字の場合
等号が2文字目になる式を解にしたいときは、1文字目に対応する数と3，4文字目に対応する数字でできる2桁の数が等しいという式でなければならなくなり、解になりません。
等号が3文字目になる式を解にしたいときも同様です。

覆面の式が5文字の場合
等号が2文字目になる式を解にしたいときは、1文字目に対応する数と3，4，5文字目に対応する数字や記号でできる数が等しいという式が解になります。
4文字目が1，3，5文字目の文字どれかと一致している覆面算では、4文字目が数字に対応して右辺が3桁の数になり、そのような式は解になりません。
よって、覆面算は「ABACA」，「ABACD」，「ABCDA」，「ABCDC」，「ABCDE」のいずれかの形をしていて、それぞれ「0＝0＋0」と「0＝0－0」，「0＝1×0」と「0＝2×0」，「0＝1×0」と「0＝2×0」，「0＝1－1」と「0＝2－2」，「3＝1＋2」と「3＝2＋1」が解になるので、別解を持ってしまいます。
等号が4文字目になる式を解にしたいときも同様です。

等号が3文字目になる式を解にしたいときは、1，2文字目に対応する数字でできる2桁の数と4，5文字目に対応する数字でできる2桁の数が等しいという式が解になります。
その覆面算が「AABAC」，「AABCA」，「ABCAA」，「ABCBB」，「AABCC」，「ABCBA」の形をしているときは解がありません。
その覆面算が「AABAA」，「ABCAB」の形をしているときは、それぞれ「11＝11」と「22＝22」，「12＝12」と「21＝21」が解になるので、別解を持ってしまいます。

等号が2つ含まれている式を考慮しても、覆面の式が5文字の場合は等号が2，4文字目になり、その覆面算は「ABABA」の形をしていて、「1＝1＝1」と「2＝2＝2」が解になるので、別解を持ってしまいます。

覆面の式が6文字の場合
2，4文字目か2，5文字目か3，5文字目が等号と四則演算記号になるような式だけが正しい等式になるので、それを導く可能性のある覆面算は次のようになります。

「ABACAA」は解なし，
「ABAACA」は解なし，
「AABACA」は解なし，
「ABACAD」は解なし，
「ABACDA」は「0＝0×10」や「0＝0×20」が解，
「ABCDAA」は解なし，
「ABCDCC」は解なし，
「ABAACD」は解なし，
「ABCADA」は「0＝10×0」や「0＝20×0」が解，
「ABCCDC」は解なし，
「AABACD」は解なし，
「AABCDA」は解なし，
「ABCBDB」は「10×0＝0」や「20×0＝0」が解，
「ABACDD」は「0＝0×11」や「0＝0×22」が解，
「ABCDAC」は解なし，
「ABCDCA」は解なし，
「ABACDC」は解なし，
「ABCADC」は解なし，
「ABCCBA」は「0＝11×0」や「0＝22×0」が解，
「AABCDC」は「11×0＝0」や「22×0＝0」が解，
「ABCADB」は解なし，
「ABCBDA」は解なし，
「ABACDE」は「0＝0×12」や「0＝0×21」が解，
「ABCDAE」は「1＋9＝10」や「－1＝2－3」が解，
「ABCDCE」は「9＋1＝10」のみが解，
「ABCDEA」は「5×3＝15」や「5×7＝35」が解，
「ABCDEC」は「3×5＝15」や「7×5＝35」が解，
「ABCDEE」は「2＋9＝11」や「9＋2＝11」が解，
「ABCADE」は「5＝15÷3」や「5＝35÷7」が解，
「ABCCDE」は「2＝11－9」や「9＝11－2」が解，
「ABCDED」は「3＝15÷5」や「7＝35÷5」が解，
「AABCDE」は「11＝2＋9」や「11＝9＋2」が解，
「ABCBDE」は「15＝5×3」や「35＝5×7」が解，
「ABCDEB」は「15＝3×5」や「35＝7×5」が解，
「ABCDEF」は「3＋9＝12」や「9＋3＝12」が解，

「ABCACA」のように、Bを＝，Cを－とすれば正しい式になる可能性がある覆面算もいくつかありますが、これらは解を持ちません。

よって、問題の覆面算は「ABCDCE」の形をしていて、「9＋1＝10」が解となります。

背景

今回のパズルの解を発見するためには、対応する式を作るのがギリギリまで苦しくなるような文字列を選ばなければなりません。
無理がなさすぎると別解が現れ，無理が過ぎると解が1つも現れなくなります。

そのため、等号である可能性が残る文字がある制限されるような文字列である必要があります。
さらに、左辺と右辺の絶妙な位置に同じ文字があることで、「9＋1＝10」だけを残すことができたのです。

今回のパズルのように、あるパズルを考えることについて考えるパズルをメタパズルといいます。
メタパズルの解に当たりをつけるときには、ギリギリを見極める力が大事になってきます。与えられたパズルを解くだけでなく、適切なパズルを作るところから始めなければならないのが「何もないパズル」の面白くて難しい部分です。

ちなみに、「－0の禁止」は数字だけを当てはめる覆面算には不要な物ですが、この自然なルールは「－0＝0」のような解答にさせないために重要な役割を持っています。
この問題の解答の左辺と右辺を入れかえた式を「－1＝2－3」型の別解がきれいに消してくれていることも奇跡的でしたが、「－0の禁止」は「－」を四則演算記号としてしか使えないような誤解をなくす役割も持たせています。