創作パズル　知りすぎ注意な数当て

はじめに

難しい論理パズルのジャンルのひとつに、登場人物が推理するパズルというものがあります。
このようなパズルを解くために賢くなければならないのは、パズルを解いている私たちだけではありません。

ある登場人物が「わからない」と言ったとき、そこから彼にわかるための情報が足りなかったのだと結論するには、彼が賢くないといけません。
賢いかわからないと、情報が足りているのに思慮が足らずにわからなかった可能性が生まれてくるからです。

そして、そう思うのもパズルを解いている私たちだけではありません。
彼の「わからない」を聞いている別の登場人物もまた推理の情報を集めているわけですから、彼が賢いということを知っていなければならないのです。
そのため、みんなが賢いことだけでなく，みんなが賢いことをみんなが知っていることも必要になってきます。

このような条件を最後までしっかりと準備しておくことで、登場人物が推理するパズルを考えることができます。

例題を見てみましょう。

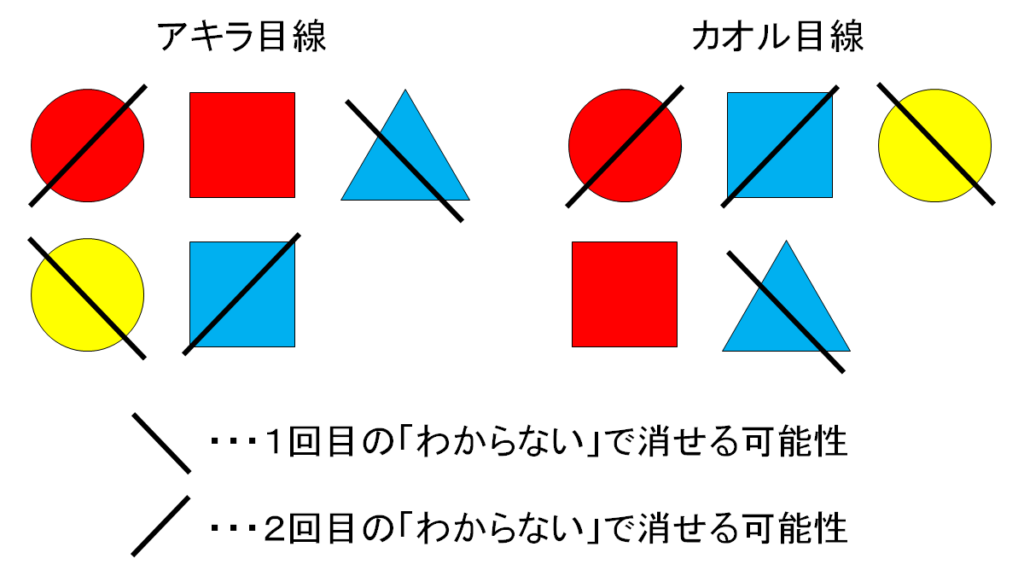
1回目のアキラの「わからない」から、(青色の)三角形ではないということが私たちとカオルにわかります。
1回目のカオルの「わからない」から、黄色(の円形)ではないということが私たちとアキラにわかります。

2回目のアキラの「わからない」から、赤色の円形ではないということが私たちとカオルにわかります。
2回目のカオルの「わからない」から、青色の四角形ではないということが私たちとアキラにわかります。

問題の条件がしっかりと準備されていれば、3回目の質問をされたときにはアキラもカオルも赤色の四角形だと答えることができます。

条件はしっかりと準備しておくことが大事です。
それを思い知ることができるパズルを作ったので、ぜひ解いてみて下さい。

考えてみよう

問題

アキラ，カオル，サツキが次のようなルールのゲームをしました。

ルール

10種類の数1，3，8，9，12，17，19，20，29，30のうち1つが選ばれる。
選ばれた数について、アキラには4で割った余り，カオルには6で割った余り，サツキには7で割った余りが教えられる。
アキラ，カオル，サツキ，アキラ，カオル，…の順に、選ばれた数がわかったかどうか発言していく。

今回のゲームでは、2周目のカオルで初めてわかったという発言がされました。
選ばれた数は何だったでしょうか？
ただし、みんな賢く，みんな賢いことをみんな知っていて，みんな賢いことをみんな知っていることもみんな知っていて，その他の余計な情報は持っていないものとします。

もし、あなたの解答が「1」になってしまったなら、問題の条件をもう一度確認することをおすすめします。

少し下にスクロールすると解答があります。

解答

3
(「賢いと知っていると知っている」を仮定から外すと解答が8に，
「賢いと知っていると知っていると知っている」を仮定に加えると解答が1に変わります。)

解説

アキラは賢いので、数が30なら1回目にわかります。…①
他の数のときは、アキラは1回目にはわかりません。

カオルは賢く，アキラが賢いと知っているので、①により数が12なら1回目にわかります。…②
他の数のときは、カオルは1回目にはわかりません。

サツキは賢いので、数が20なら1回目にわかります。…③
サツキは賢く，アキラが賢いと知っているので、①により数が9なら1回目にわかります。…④
サツキは賢く，カオルが賢いと知っていて，アキラが賢いとカオルが知っていると知っているので、②により数が19なら1回目にわかります。…⑤
他の数のときは、サツキは1回目にはわかりません。

アキラは賢く，カオルが賢いと知っていて，アキラが賢いとカオルが知っていると知っていて，サツキが賢いと知っているので、②と③により数が8なら2回目にわかります。…⑥
他の数のときは、アキラは2回目にはわかりません。

カオルは賢く，サツキが賢いと知っていて，アキラが賢いとサツキが知っていると知っているので、④により数が3なら2回目にわかります。…⑦
他の数のときは、カオルは2回目にはわかりません。

よって、今回のゲームで選ばれた数は3です。

背景

この問題の条件は「賢いと知っていると知っている」までなので、「賢いと知っていると知っている」を使った推理は登場人物には不可能です。
例えば、2回目のカオルの推理で「1ならカオルはわかるのでは？」と考えた人も多いと思いますが、実際は次のようにカオルにはわかりません。
カオルは賢く，サツキが賢いと知っていて，カオルが賢いとサツキが知っていると知っていますが、アキラが賢いとカオルが知っているとサツキが知っているとは知らないので、⑤を使うことができず、数が1なら数が19かもしれないままなので2回目にはわかりません。

登場人物も推理するパズルに慣れている人ほど「知りすぎ」な条件で解いてしまったのではないでしょうか。
推理することに慣れてしまうと、その推理が何を根拠に成り立っているのか確認するのがおろそかになってしまいがちです。

この問題は、条件の強さを読み間違えると正答に到達できないだけでなく、別の結果に到達してしまうように作りました。
条件を変えたときに解答が1や8に変わる様子も楽しんでもらえたらと思います。

賢いかどうか，それを知っているかどうかは、このようなパズルにおいては前提としていて省略されていることもよくあります。
すべてが省略されているなら、それらがすべて仮定されていると思ってもいいと思います。
しかし、この問題のように中途半端なところまで書かれていた場合は、さすがに「賢いと知っていると知っていると知っている」は仮定されていないとみなすべきでしょう。
では、記事のはじめに出てきた例題は、どう解くべきだったといえるでしょうか……？