目次
はじめに
てくますプロジェクトでは、てくますゼミと呼ばれる輪読会を隔週で開催しています。
少人数であーだこーだ議論しながら、考える楽しさを分かち合う、ゼミのようなコミュニティです。主に、AIなどの「IT × 数学」領域について学習しています。

現在は「ゼロから作るDeep Learning」というディープラーニングの有名な本を読み進めています。
今回は本書第4回の輪読会ということで、5章を読み進めました!
本記事では、今回の勉強会で学んだことをざっくりと紹介していきます。
学習内容(5章)
前章のおさらい
ニューラルネットワークの学習では、勾配法を用いて、損失関数の値が最も小さくなる重みパラメータを探すのでした。
勾配法とは、グラフの今いる点の勾配(各重みパラメータによる偏微分係数を並べて出来るベクトル)に沿って下っていくことで、最小値を探す手法です。
前の章では、数値微分を用いて勾配を計算しました。しかし数値微分には、計算に時間がかかるという難点があります。そこで本章では微分の計算の工夫として、誤差逆伝播法を学びました。
誤差逆伝播法のこころ
例として、\(z=(x+y)^2\) を考えます。
この式は次のように分解できます。
\(z=t^2\)
\(t=x+y\)
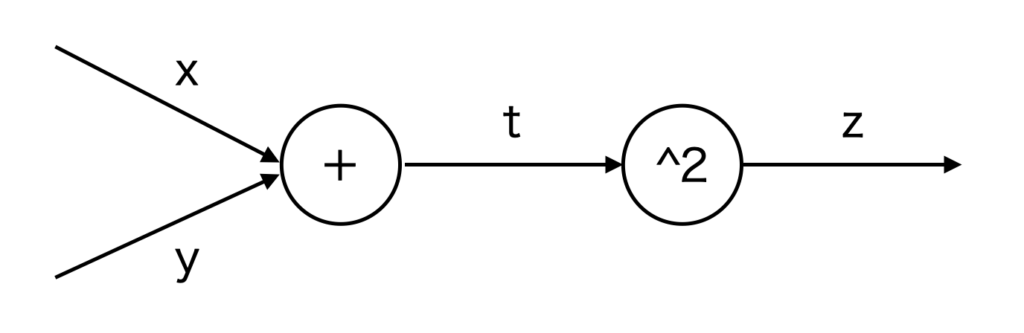
求めたいものは、各パラメータ \(t, x, y\) を微小に変化させたときのzの変化率、
すなわち、\(\displaystyle\frac{\partial z}{\partial t}, \frac{\partial z}{\partial x}, \frac{\partial z}{\partial y}\) です。
\(z=t^2\) なので、 \(\displaystyle\frac{\partial z}{\partial t}=2t\) です。
\(\displaystyle\frac{\partial z}{\partial x}, \frac{\partial z}{\partial y}\) は連鎖律(合成関数の微分法)によって求めることができます。
\(\displaystyle\frac{\partial z}{\partial x} = \frac{\partial z}{\partial t} \cdot \frac{\partial t}{\partial x} = 2t \cdot 1 = 2t\)
\(\displaystyle\frac{\partial z}{\partial y} = \frac{\partial z}{\partial t} \cdot \frac{\partial t}{\partial y} = 2t \cdot 1 = 2t\)
\(\displaystyle\frac{\partial z}{\partial x}, \frac{\partial z}{\partial y}\) を求めるのに、一つ前で求めた \(\displaystyle\frac{\partial z}{\partial t}\) を用いています。
このように、後ろの層から微分の計算を行い、その計算を前の層で再利用します。これが後ろから計算する理由であり、逆伝播の名前の由来です。
逆伝播では、右から左へと信号を伝播させます。その際に、そのノードでの局所的な微分をかけ算して、次のノードに移動します。
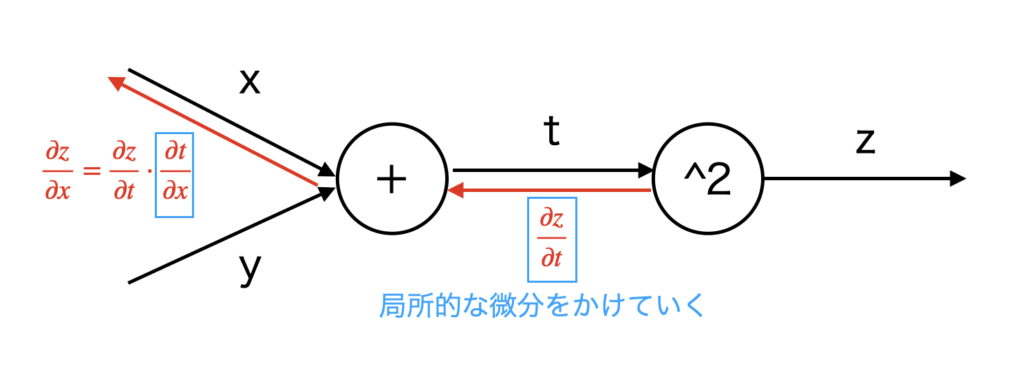
前章では、\(\displaystyle\frac{\partial z}{\partial x}\) を直接、数値微分で計算しようとしていたのに対し、今章の誤差逆伝播法では、連鎖律を用いて後ろのノードから逐次的に計算しています。これによって微分の計算が効率的に行えるというわけです。
テキストではこの考え方を用いて、ニューラルネットワークを構成するレイヤ(ReLUレイヤ、Sigmoidレイヤ、Affineレイヤ、Softmaxレイヤ)の実装を行っています。それらについては頑張って計算していくのみですので、ここでは割愛します。
最後に
何となくでしか知らなかった「誤差逆伝播法」を今回学ぶことができて嬉しかったです。輪読会では、何のための「逆」なのかなどの話題で盛り上がりました。
本書の輪読会も残すはあと2回。少しゴールが見えてきましたね。
では、また!






