創作パズル　落書きパズル―再びの落書き―

はじめに

落書き型論理パズルの第2弾を紹介します。

2023.09.18

「はじまりの落書き」で落書き型論理パズルの考え方を身に付けたら、その考え方をうまく使って難しいパズルに挑戦してみましょう！

考えてみよう

問題

アキラ，カオル，サツキ，タクミ，ナギサはいたずら好きの仲良し5人組です。
5人は今日、それぞれが学校に到着したときに塀に1つずつ落書きをしてから教室に入りました。
到着したとき先に書かれている落書きは読めますが、落書きなので筆跡からは書かれた順番や書いた人はわかりません。
5人は十分に賢く、昨日の5人の到着順は全て知っていて、これらの情報だけを前提として推理して落書きをしました。

「今日のアキラとカオルのどちらの到着が先かわかった」
「今日のカオルとサツキのどちらの到着が先かわかった」
「昨日のサツキとタクミの到着順は2つだけ違っていた」
「昨日より今日の到着順が後ろになる人が2人以上いるとわかった」
「まだ全員到着していないが、今日の全員の到着順がわかった」

落書きがこの5つのとき、昨日と今日それぞれの到着順に5人を並べてください。

落書きに書いてある情報、すごく少なくない……？
それなのに、2日分の到着順なんてわかるの？

「○○だとわかった」には想像以上の量の情報が詰まっているから大丈夫です。

少し下にスクロールすると解答があります。

解答

昨日…アキラ，タクミ，カオル，サツキ，ナギサ
今日…カオル，ナギサ，サツキ，アキラ，タクミ

解説

落書きを上から順にA，B，C，D，Eと呼ぶことにします。
カオル，アキラがそれぞれ昨日のx，y番目であるとき、Aをx-yと表すことにします。
カオル，サツキがそれぞれ昨日のx，y番目であるとき、Bをx-yと表すことにします。

x-yが1番目に書かれているならば、今日の1番目は昨日のxかy番目になります。
今日の1番目が昨日のx番目でもy番目でもないなら、その人にとって、今日は昨日のx，y番目のうちどちらが先に到着したかわからないので、x-yと書けないからです。
逆に、今日の1番目が昨日のxかy番目なら、その人にとって、今日は自分が先に到着したとわかるので、x-yと書くことができます。

Dは1番目に書かれていません。
今日の1番目が昨日のx番目だとおくと、その人にとって、昨日の1番目とx番目以外の順番が変わっておらず1人以下しか順番が後ろになっていない可能性があって、Dと書けないからです。

Eは4番目に書かれています。
今日の3番目以前の人にとって、今日の4番目はまだ到着していないどちらの人である可能性もあるので、Eと書けません。
そして、Eの内容により、5番目でもないからです。

Cは5番目に書かれています。
誰でも書けるCが5番目でないなら、今日の4番目にとって、Cを書いた人とまだ到着していない5番目の人を区別できず、Eと書けなくなってしまうからです。

3番目までの落書きは、順不同でx-y，x-z，D(y<zとしてよい)となります。
x，y，zの場合分けごとに、今日の1，2，3番目がそれぞれ昨日の何番目である可能性があるか表にまとめます。
表のwは、カッコに書かれている条件をみたす昨日の順番ならどの順番である可能性もあります。

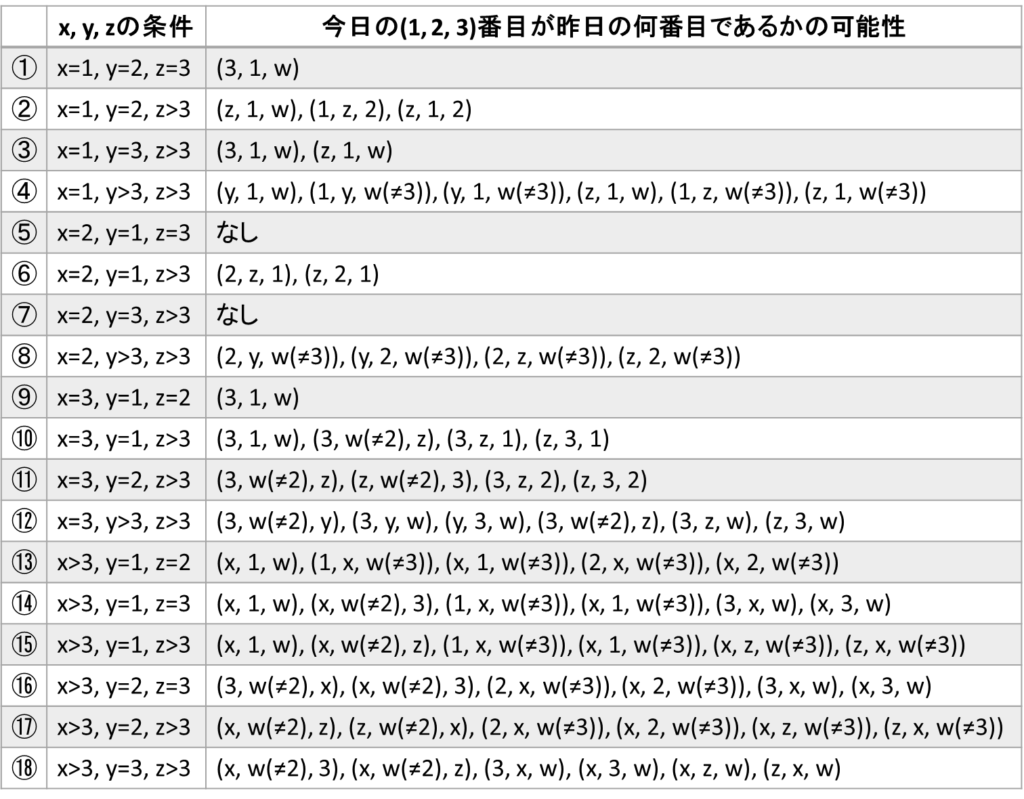
⑩のx=3，y=1，z>3で今日の4番目が昨日の1番目のときだけ、今日の4番目はEと書けます。
今日の4番目は今日の1，2，3番目を考えるとき、AやBに書かれた名前の人が昨日何番目だったのか知っているので①～⑱のどの状況か知っていて、さらにその右に列挙した可能性のうち今日の4番目の昨日の順番が含まれているものを除外することができます。
①～⑱の1つに制限して、今日の4番目の昨日の順番が含まれているものを除外しても複数の可能性が残ると、今日の4番目はそれらを区別できず、Eと書けなくなります。
また、条件の付いていないwが使われている可能性が残ると、その可能性内の他の2つの順番と今日の4番目の昨日の順番を除いてもwには2通り以上の可能性が残り、今日の4番目はそれらを区別できず、Eと書けなくなります。
よって、⑩の状況で今日の4番目が昨日の1番目のときだけ、今日の4番目にとって今日の順番が「昨日の3番目，残り，昨日のz番目，自分，昨日の2番目」だとわかり、Eと書くことができます。

カオルを昨日のx番目としていたので、カオルは昨日の3番目で今日の1番目となります。

アキラは昨日の1番目で今日の4番目となります。
アキラが昨日のz番目なら、サツキが昨日の1番目となり、カオルが昨日の3番目なのでCに書かれていることに反するからです。

サツキは昨日の4番目で今日の3番目となります。
サツキが昨日のz番目となるわけですが、z=1なら、カオルが昨日の3番目なのでCに書かれていることに反するからです。

Cの内容により、タクミは昨日の2番目で今日の5番目となります。

ナギサは昨日の5番目で今日の2番目となります。

ゆえに、昨日はアキラ，タクミ，カオル，サツキ，ナギサの順番で到着していて、今日はカオル，ナギサ，サツキ，アキラ，タクミの順番で到着していて、落書きはB，D，A，E，Cの順に書かれたとわかります。

背景

「再びの落書き」は落書き型論理パズルの第2弾です。
みなさんにとっては”再び”となる落書きパズルであり、登場人物にとっては昨日をふまえて”再び”の到着順について考えているパズルなので、このようなサブタイトルにしました。

落書きに書かれた直接的な条件に比べて、「わかった」からわかる間接的な条件には想像以上の量の情報が詰まっていることがあります。
結局どっちが先に到着したのかも教えてくれない上2つの落書きをはじめとして、今回のパズルには直接的な条件を与えてくれる落書きはほとんどありません。
それにもかかわらず、今回は5人の昨日と今日の順番を特定することまでできてしまうのです。
このパズルを通して、間接的な条件が持つ力を感じてもらえればと思います。

今回のパズルは美しさの面で特にお気に入りなので、残りはその美しさについて語ろうと思います。
論理パズルの解を1通りにするためには、問題文で登場人物を非対称にする必要があります。
例えば、問題文でアキラとカオルが全く同じに扱われていたとしたら、解くときにアキラとカオルを区別できないので解が1通りになりません。
今回のパズルでは、5人を非対称にするための最低限の文章でしか、5人に個別には触れていないことがわかります。