目次
はじめに
落書き型論理パズルというものを考案しました。
解くことの難しさだけでなく、普段はあまり大事にされていない推理要素の活躍にも注目して、この問題をお楽しみください!
考えてみよう
問題
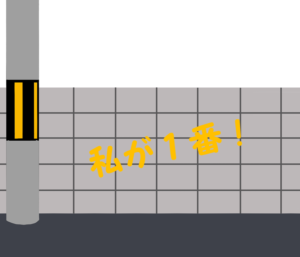
一番上の落書きがあれば、他の落書きは必要ないような……?
これだと、最後がアキラということしかわからないのでは?
いいえ、落書きの主張が「○○だとわかった」なのがポイントなのです。
少し下にスクロールすると解答があります。
解答
サツキ,タクミ,カオル,アキラ
解説
落書きを上から順にA,B,C,Dと呼ぶことにします。
Dは内容から、4番目に書かれています。…※
サツキが1番目だとすると、サツキにとってはタクミが4番目かもしれないのでAやBを書けません。
サツキ以外が1番目だとすると、その人にとってはサツキが4番目かもしれないのでAやBやCを書けません。
よって、1番目はサツキでCを書いていなければいけません。
実際、サツキが1番目ならCを書くことができます。
ここまでの話は※を除いて、2番目に来てCを見た人も推理できることに注意しましょう。
タクミが2番目だとすると、タクミとってはカオルが4番目かもしれないのでAを書けません。
タクミ以外が2番目だとすると、その人にとってはタクミが4番目かもしれないのでAやBを書けません。
よって、2番目はタクミでBを書いていなければいけません。
実際、タクミが2番目ならBを書くことができます。
ここまでの話は※を除いて、3番目に来てBとCを見た人も推理できることに注意しましょう。
Aの内容から、4番目はアキラで3番目はカオルでなければなりません。
ゆえに、サツキ,タクミ,カオル,アキラの順番で到着していて、落書きはC,B,A,Dの順になります。
実際、カオルが3番目でA,アキラが4番目でDを書くことができます。
背景
よくある論理パズルでは、解答が満たさなければならない条件がいくつか教えられます。
そのすべてを満たすような状況を見つけることが、そのパズルを解くということです。
例えば、「アキラが最後」という条件は、問題を解く私たちに手掛かりを与えてくれます。
しかし、その条件はその情報しか私たちに与えてくれません。
ここで、「アキラが最後」という情報がカオルから私たちに与えられたとしたらどうでしょうか?
適切な設定のもとなら、「アキラが最後だとカオルにわかるような状況だ」という情報も得ることができます。
登場人物も推理していて推理の結論だけでなく推理の過程も情報とするパズルでは、誰がそれを言ったのか,いつそれを言ったのかまでもが重要になってきます。
それらはとても大事で、そのありがたさを知ってもらいたくて、消すことにしました。
消えているのは要らないからではありません。
それがこの落書き型論理パズルです。
今回は、「アキラかカオルが最後」や「サツキが最後ではない」という「アキラが最後」の情報に含まれてしまっている情報や、「私が最後」という私たちが必要としていない情報ばかりを並べ、それらがしっかり活躍する問題を作ることにしました。
最後に
「はじまりの落書き」なのに、みんな最後の到着のことしか話していないというのはご愛敬。
「落書きパズル」シリーズはいくつかあるので、他も楽しみにしていてください。
この記事もオススメ
落書きパズルシリーズはこちら。
推理を推理するパズルはこちら。












アキラ,カオル,サツキ,タクミはいたずら好きの仲良し4人組です。
4人は、それぞれが学校に到着したときに塀に1つずつ落書きをしてから教室に入りました。
到着したとき先に書かれている落書きは読めますが、落書きなので筆跡からは書かれた順番や書いた人はわかりません。
4人は十分に賢く、これらの情報だけを前提として推理して落書きをしました。
「アキラの到着が最後だとわかった」
「アキラかカオルの到着が最後だとわかった」
「サツキの到着が最後ではないとわかった」
「私の到着が最後だとわかった」
落書きがこの4つのとき、4人を到着順に並べてください。